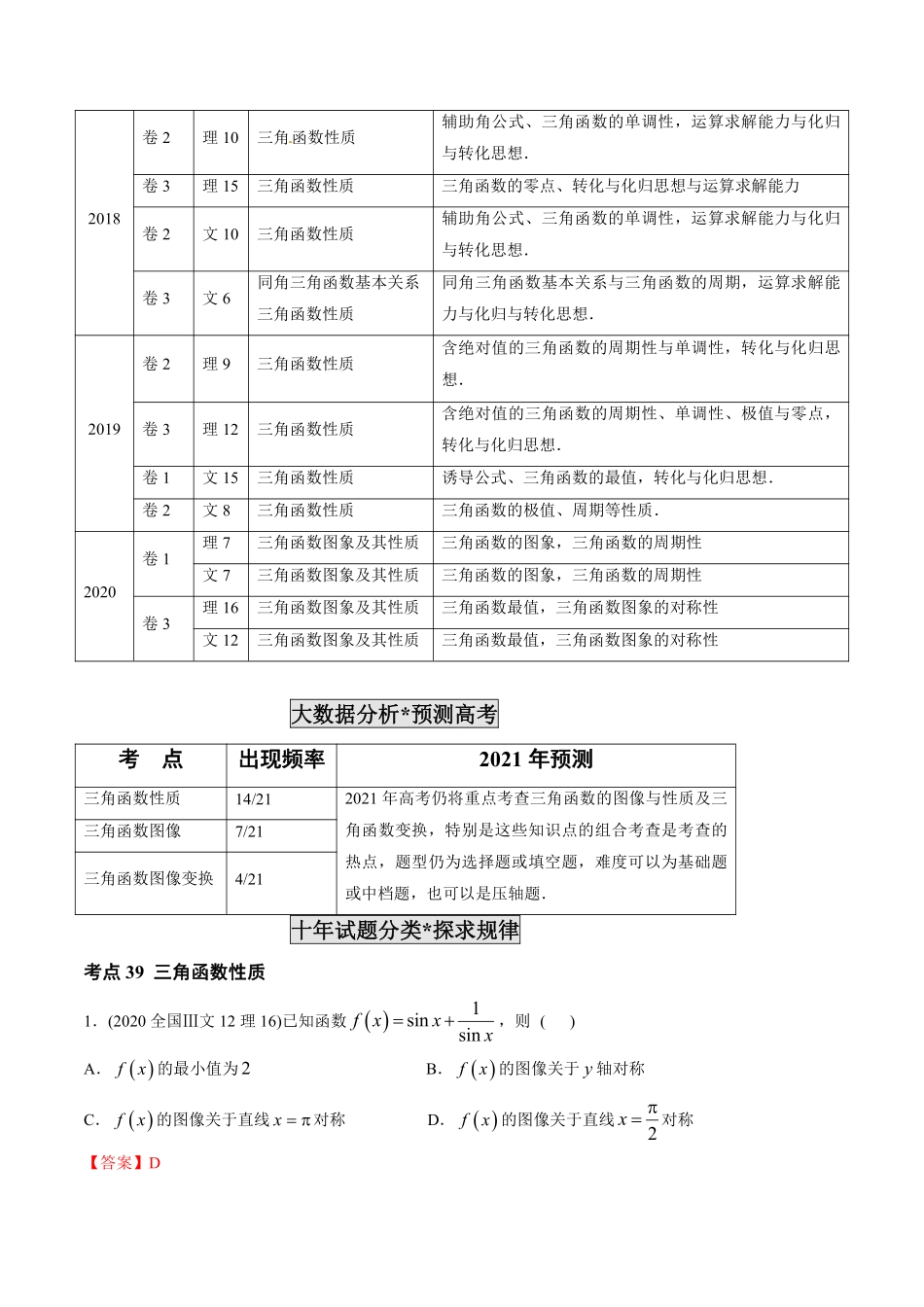
专题12三角函数图象与性质十年大数据*全景展示年份题号考点考查内容2011[来源:学科网]课标理11三角函数性质[来源:学科网]三角函数的周期性、奇偶性、单调性[来源:学科网]课标文11三角函数性质三角公式、诱导公式、三角函数的性质及分析处理问题能力.2012课标理9三角函数性质三角函数的单调性课标文9三角函数性质三角函数的对称轴等性质2013卷2文16三角函数图像变换三角函数图像平移变换2014卷1文7三角函数图像本三角函数的周期性.2015卷1理8文8三角函数图像已知三角函数图像求解析式及三角函数的单调性.2016卷3理14三角函数图像变换两角和与差的三角公式及图像平移变换.卷1文6三角函数图像变换三角函数周期、三角函数的平移变换.卷2文3三角函数图像已知三角函数图像求解析式卷3文14三角函数图像辅助角公式及三角函数平移变换.2017卷1理9三角函数图像变换诱导公式、三角函数图像变换,化归与转化思想卷3理6三角函数性质三角函数周期、对称性、零点与单调性.卷2文3三角函数性质三角函数周期性2018卷2理10三角函数性质辅助角公式、三角函数的单调性,运算求解能力与化归与转化思想.卷3理15三角函数性质三角函数的零点、转化与化归思想与运算求解能力卷2文10三角函数性质辅助角公式、三角函数的单调性,运算求解能力与化归与转化思想.卷3文6同角三角函数基本关系三角函数性质同角三角函数基本关系与三角函数的周期,运算求解能力与化归与转化思想.2019卷2理9三角函数性质含绝对值的三角函数的周期性与单调性,转化与化归思想.卷3理12三角函数性质含绝对值的三角函数的周期性、单调性、极值与零点,转化与化归思想.卷1文15三角函数性质诱导公式、三角函数的最值,转化与化归思想.卷2文8三角函数性质三角函数的极值、周期等性质.2020卷1理7三角函数图象及其性质三角函数的图象,三角函数的周期性文7三角函数图象及其性质三角函数的图象,三角函数的周期性卷3理16三角函数图象及其性质三角函数最值,三角函数图象的对称性文12三角函数图象及其性质三角函数最值,三角函数图象的对称性大数据分析*预测高考考点出现频率2021年预测三角函数性质14/212021年高考仍将重点考查三角函数的图像与性质及三角函数变换,特别是这些知识点的组合考查是考查的热点,题型仍为选择题或填空题,难度可以为基础题或中档题,也可以是压轴题.三角函数图像7/21三角函数图像变换4/21十年试题分类*探求规律考点39三角函数性质1.(2020全国Ⅲ文12理16)已知函数...