2009年全国硕士研究生入学统一考试数学一真题(1).pdfVIP免费

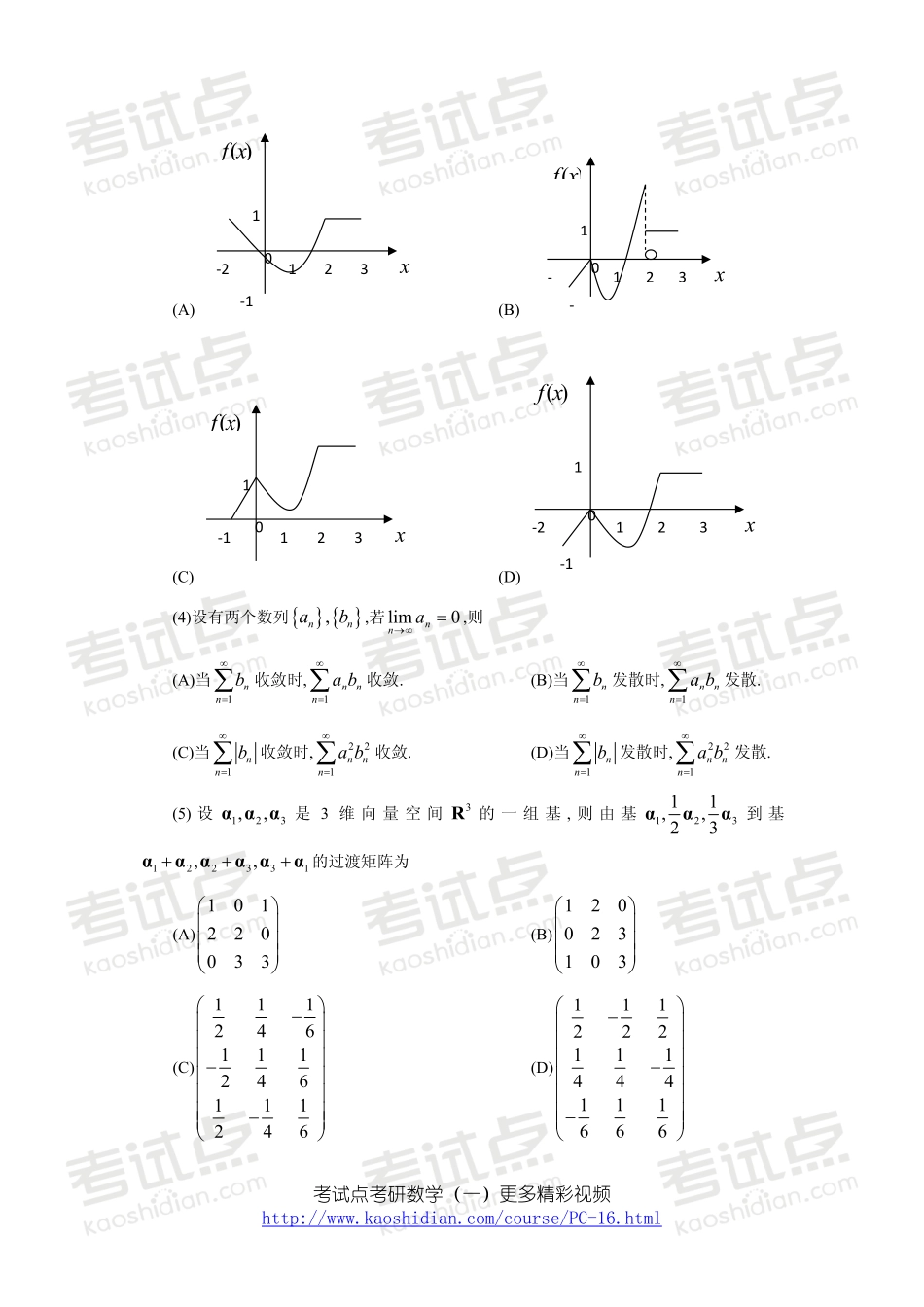
考试点考研数学（一）更多精彩视频http://www.kaoshidian.com/course/PC-16.html2009年全国硕士研究生入学统一考试数学(一)试卷一、选择题(1-8小题,每小题4分,共32分,下列每小题给出的四个选项中,只有一项符合题目要求,把所选项前的字母填在题后的括号内.)(1)当0x时,sinfxxax与2ln1gxxbx等价无穷小,则(A)11,6ab(B)11,6ab(C)11,6ab(D)11,6ab(2)如图,正方形,1,1xyxy被其对角线划分为四个区域1,2,3,4kDk,coskkDIyxdxdy,则14maxkkI(A)1I(B)2I(C)3I(D)4I(3)设函数yfx在区间1,3上的图形为则函数0xFxftdt的图形为1()fx-2023x-1O考试点考研数学（一）更多精彩视频http://www.kaoshidian.com/course/PC-16.html(A)()fx023x1-2-11(B)()fx023x1--1(C)()fx023x1-11(D)()fx023x1-2-11(4)设有两个数列,nnab,若lim0nna,则(A)当1nnb收敛时,1nnnab收敛.(B)当1nnb发散时,1nnnab发散.(C)当1nnb收敛时,221nnnab收敛.(D)当1nnb发散时,221nnnab发散.(5)设123,,ααα是3维向量空间3R的一组基,则由基12311,,23ααα到基122331,,αααααα的过渡矩阵为(A)101220033(B)120023103(C)111246111246111246(D)111222111444111666考试点考研数学（一）更多精彩视频http://www.kaoshidian.com/course/PC-16.html(6)设,AB均为2阶矩阵,**,AB分别为,AB的伴随矩阵,若2,3AB,则分块矩阵OABO的伴随矩阵为(A)**32OBAO(B)**23OBAO(C)**32OABO(D)**23OABO(7)设随机变量X的分布函数为10.30.72xFxx,其中x为标准正态分布函数,则EX(A)0(B)0.3(C)0.7(D)1(8)设随机变量X与Y相互独立,且X服从标准正态分布0,1N,Y的概率分布为1012PYPY,记ZFz为随机变量ZXY的分布函数,则函数ZFz的间断点个数为(A)0(B)1(C)2(D)3二、填空题(9-14小题,每小题4分,共24分,请将答案写在答题纸指定位置上.)(9)设函数,fuv具有二阶连续偏导数,,zfxxy,则2zxy.(10)若二阶常系数线性齐次微分方程0yayby的通解为12exyCCx,则非齐次...