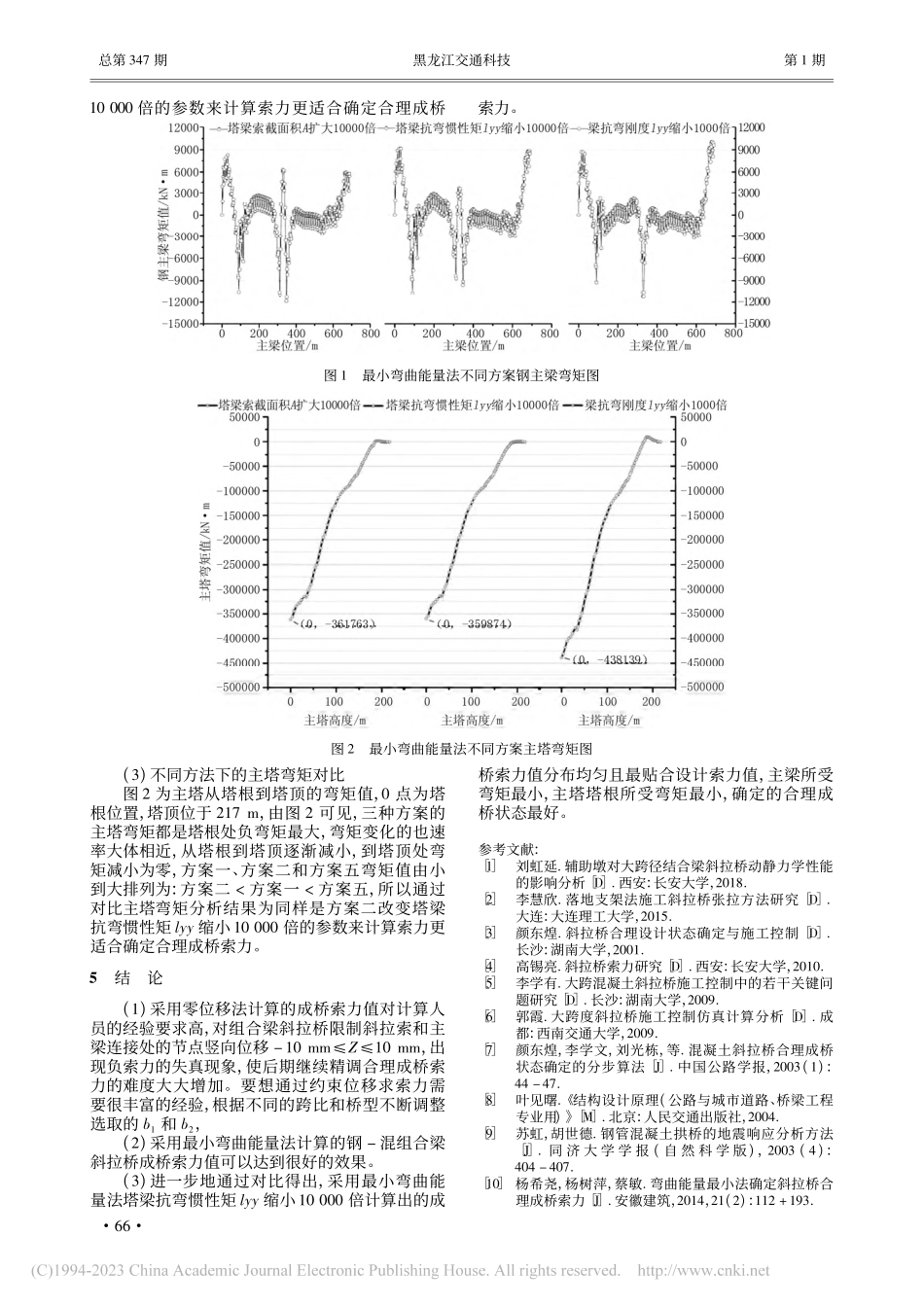
2023年第1期(总第347期)黑龙江交通科技HEILONGJIANGJIAOTONGKEJINo.1,2023(SumNo.347)组合梁斜拉桥的合理成桥索力计算方法研究戴明禹(无锡地铁建设有限责任公司,江苏无锡214000)摘要:确定斜拉桥合理成桥状态下的索力是设计和计算分析的关键,以赤壁长江公路大桥为工程背景,对零位移法和不同设置参数下的最小弯曲能量法的电算结果进行分析和比较,探究适合组合梁斜拉桥合理成桥索力的初步确定方法。结果表明:最小弯曲能量法使塔梁抗弯惯性矩lyy缩小10000倍的参数来计算,得到的合理成桥状态方案最优。关键词:组合梁斜拉桥;合理成桥状态;成桥索力优化中图分类号:U442文献标识码:A文章编号:1008-3383(2023)01-0064-03ResearchontheDeterminationMethodofReasonableFinishedCableForceofCompositeBeamCable-stayedBridgeDAIMing-yu(WuxiMetroConstructionCo.,Ltd.,Wuxi,Jiangsu214000,China)Abstract:Itisthekeytodeterminethecableforceofacable-stayedbridgeunderreasonablecompletioncondition.TakingaYangtzeRiverHighwayBridgeastheengineeringbackground,thispaperanalyzesandcomparestheresultsofthezerodisplacementmethodandtheminimumbendingenergymethodunderdifferentsettingparameterstoexplorethepreliminarydeterminationmethodsuitableforthereasonablecompletioncableforceofthecompositegirdercable-stayedbridge.Theresultsshowthattheminimumbendingenergymethodreducesthebendinginertiamomentlyyofthetowergirderby10000times,andthereasonablefinisheddeadstateisoptimal.Keywords:compositebeamcable-stayedbridge;reasonablefinisheddeadstate;cableforceoptimization收稿日期:2022-01-11作者简介:戴明禹(1992—),男,江苏高邮人,硕士,助理工程师,研究方向:桥梁与隧道工程0引言合理的成桥状态是斜拉桥设计过程的开始,然后以要确定的成桥状态为目标,根据现实中的施工过程,采用工程控制手段以达到预定的桥梁状态[1]。因此,设计和计算分析的关键点是确定斜拉桥的合理桥梁状态。判断斜拉桥方案是否合理的标准之一是成桥状态下全桥内力分布的情况[2]。确定合理成桥状态时,索力应满足:塔要直:恒定荷载作用时,索塔尽量承受轴向压力,弯矩不应太大[3];主梁要平:在成桥状态下,主梁的弯矩尽量比较均匀,控制在“可行域”范围内[4]。索力变化要均匀:全桥索力的分布要均衡,不应当出现过...