课时3287_8.6.3平面与平面垂直（第2课时）-8.6.3 平面与平面垂直(第二课时)【公众号dc008免费分享】.pptxVIP免费

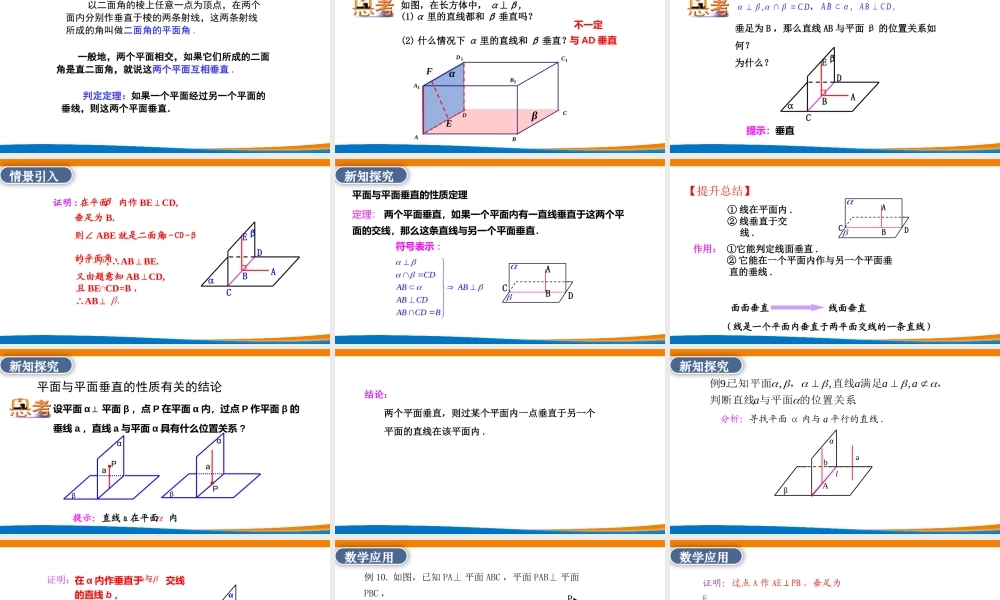
（第二课时）主讲人：光明区高级中学郭子业深圳市新课程新教材高中数学在线教学8.6.3平面与平面垂直温故知新以二面角的棱上任意一点为顶点，在两个面内分别作垂直于棱的两条射线，这两条射线所成的角叫做二面角的平面角.一般地，两个平面相交，如果它们所成的二面角是直二面角，就说这两个平面互相垂直.判定定理：如果一个平面经过另一个平面的垂线，则这两个平面垂直．A1D1B1C1CBADαβEF如图，在长方体中，α⊥β,(1)α里的直线都和β垂直吗？(2)什么情况下α里的直线和β垂直？与AD垂直不一定情景引入垂足为B，那么直线AB与平面β的位置关系如何？为什么？,CD，,ABαβABDCE,ABCD提示：垂直情景引入证明:在平面内作BECD,⊥ ,ABBE.∴⊥又由题意知ABCD,⊥且BECD=B，β垂足为B.∴AB⊥.则∠ABE就是二面角的平面角.α-CD-βαβABDCE情景引入平面与平面垂直的性质定理符号表示:CDABABABCDABCDBDCAB定理：两个平面垂直，如果一个平面内有一直线垂直于这两个平面的交线，那么这条直线与另一个平面垂直．新知探究（线是一个平面内垂直于两平面交线的一条直线）面面垂直线面垂直作用：①它能判定线面垂直.②它能在一个平面内作与另一个平面垂直的垂线.关键点：①线在平面内.②线垂直于交线.DCAB【提升总结】平面与平面垂直的性质有关的结论设平面α⊥平面β，点P在平面α内，过点P作平面β的垂线a，直线a与平面α具有什么位置关系?a提示：直线a在平面内βαPβαPa新知探究两个平面垂直，则过某个平面内一点垂直于另一个平面的直线在该平面内.结论：bαβAal分析：寻找平面α内与a平行的直线..,,,.9的位置关系与平面判断直线，满足直线，已知平面例aaaa新知探究在α内作垂直于交线的直线b， ∴又∴ab.∥又∴aα.∥即直线a与平面α平行.，b，a，a，结论：垂直于同一平面(β)的直线(a)和平面(α)平行（）aβbαAal与证明：例10.如图，已知PA⊥平面ABC，平面PAB⊥平面PBC，求证：BC⊥平面PAB.EPABC分析：要证明BC⊥平面PAB，需证明BC垂直于平面PAB内的两条相交直线.由已知条件易得BC⊥PA.再利用平面PAB⊥平面PBC，过点A作PB的垂线AE，由两个平面垂直的性质可得BC⊥AE.数学应用PABCE PA⊥平面ABC，BC平面ABC,∴PA⊥BC.又PA∩AE=A,∴BC⊥平面PAB证明：过点A作AE⊥PB，垂足为E， 平面PAB⊥平面PBC，平面PAB∩平...