课时3243_6.3.3平面向量加 减运算的坐标表示-6.3.3平面向量加、减运算的坐标表示【公众号dc008免费分享】.pptxVIP免费

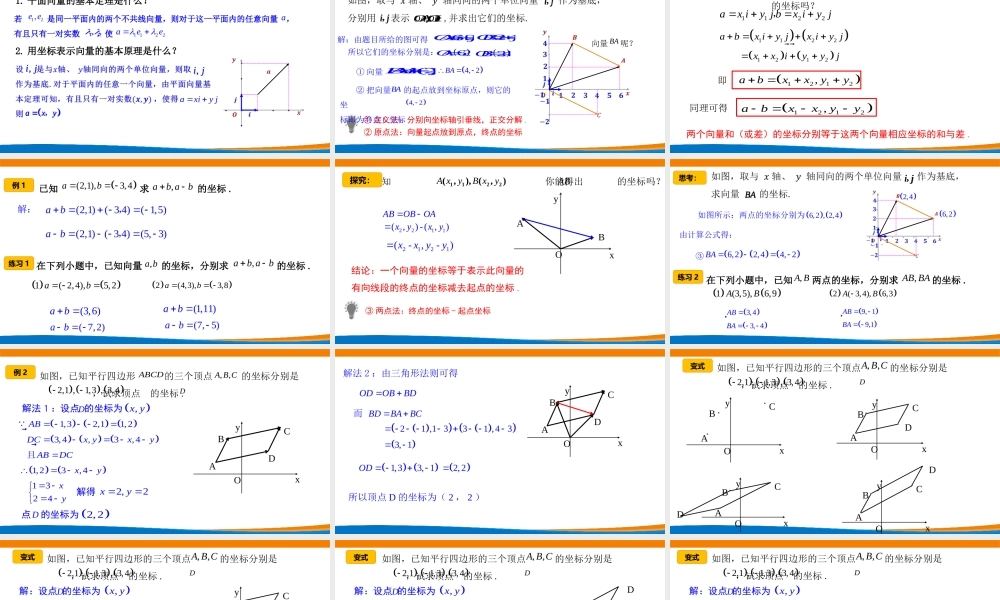
主讲人：深圳市宝安中学（集团）高中部刘晓深圳市新课程新教材高中数学在线教学6.3.3平面向量加、减运算的坐标表示1.平面向量的基本定理是什么？2.用坐标表示向量的基本原理是什么？复习回顾··········若是同一平面内的两个不共线向量，则对于这一平面内的任意向量，有且只有一对实数，使12,ee�12,1122aee��a,ij,ijaxy，axiyj,ij,ijaxy，·······情境引入①定义法：分别向坐标轴引垂线，正交分解.②原点法：向量起点放到原点，终点的坐标4,2BA�向量呢？BA�②把向量的起点放到坐标原点，则它的坐标即为终点C坐标4,2BA�①向量4(2)BAij�解：由题目所给的图可得62OAij�24OBij�所以它们的坐标分别是：24OB�，62OA�，ij，ij，,OAOB�ij，ij，,OAOB�两个向量和（或差）的坐标分别等于这两个向量相应坐标的和与差.11221212abxiyjxiyjxxiyyj即1212,abxxyy已知，你能得到的坐标吗？1122(,),(,)axybxybaba,思考：同理可得1212,abxxyy1122axiyjbxiyj，解：(2,1)(34)(1,5)ab，(2,1)(34)(5,3)ab，已知求的坐标.(2,1),3,4ab,abab(3,6)ab(7,2)ab(1,11)ab(7,5)ab例1,abab,ab在下列小题中，已知向量的坐标，分别求的坐标.1(2,4),5,2ab2(4,3),3,8ab练习1如图，已知你能得出的坐标吗？AxyBxy1122(,),(,)AB�xyOBAABOBOA�2211(,)-(,)xyxy2121(-,-)xxyy结论：一个向量的坐标等于表示此向量的有向线段的终点的坐标减去起点的坐标.探究：③两点法：终点的坐标-起点坐标·············③6,22,44,2BA�6,22,4思考：如图所示：两点的坐标分别为由计算公式得：6,2,2,4BA�ij，3,43,4ABBA��9,19,1ABBA��,ABBA�,AB在下列小题中，已知两点的坐标，分别求的坐标.1(3,5),6,9AB2(3,4),6,3AB练习2BA�ij，ABCDxyO1,32,11,23,4,3,4ABDCxyxyABDC���且解得2,2xy...