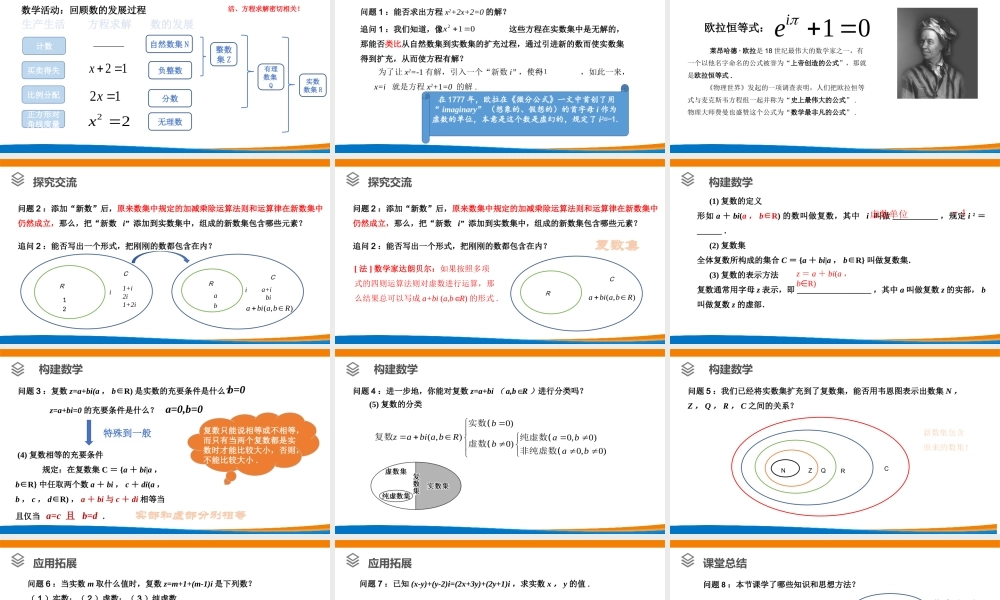
主讲人:深圳市翠园中学魏燕婷深圳市新课程新教材高中数学在线教学7.1.1数系的扩充和复数的概念数学活动:回顾数的发展过程生产生活方程求解数的发展计数买卖得失比例分配正方形对角线度量21x22x21x自然数集N负整数分数无理数整数集Z有理数集Q实数数集R—————结论:数的发展与生产生活、方程求解密切相关!情境导入探究交流追问1:我们知道,像这些方程在实数集中是无解的,那能否类比从自然数集到实数集的扩充过程,通过引进新的数而使实数集得到扩充,从而使方程有解?210x为了让x2=-1有解,引入一个“新数i”,使得,如此一来,x=i就是方程x2+1=0的解.12i在1777年,欧拉在《微分公式》一文中首创了用“imaginary”(想象的、假想的)的首字母i作为虚数的单位,本意是这个数是虚幻的,规定了i2=-1.问题1:能否求出方程x2+2x+2=0的解?欧拉恒等式:莱昂哈德·欧拉是18世纪最伟大的数学家之一,有一个以他名字命名的公式被誉为“上帝创造的公式”,那就是欧拉恒等式.《物理世界》发起的一项调查表明,人们把欧拉恒等式与麦克斯韦方程组一起并称为“史上最伟大的公式”.物理大师费曼也盛赞这个公式为“数学最非凡的公式”.探究交流10ie探究交流RC11+i2i1+2iRC),(Rbabiai2追问2:能否写出一个形式,把刚刚的数都包含在内?问题2:添加“新数”后,原来数集中规定的加减乘除运算法则和运算律在新数集中仍然成立,那么,把“新数i”添加到实数集中,组成的新数集包含哪些元素?abia+ibi探究交流RC),(Rbabia[法]数学家达朗贝尔:如果按照多项式的四则运算法则对虚数进行运算,那么结果总可以写成a+bi(a,bR∈)的形式.复数集追问2:能否写出一个形式,把刚刚的数都包含在内?问题2:添加“新数”后,原来数集中规定的加减乘除运算法则和运算律在新数集中仍然成立,那么,把“新数i”添加到实数集中,组成的新数集包含哪些元素?构建数学(1)复数的定义形如a+bi(a,b∈R)的数叫做复数,其中i叫做___________,规定i2=______.(2)复数集全体复数所构成的集合C={a+bi|a,b∈R}叫做复数集.(3)复数的表示方法复数通常用字母z表示,即__________________,其中a叫做复数z的实部,b叫做复数z的虚部.虚数单位-1z=a+bi(a,b∈R)构建数学问题3:复数z=a+bi(a,b∈R)是实数的充要条件是什么?a=0,b=0复数只能说相等或不相等,而只有当两个复数都是实数时才能比较大小,否则,不能比较大小.z=a+bi=0的充要条件是什么?b=0(4...