课时3238_6.2.4向量的数量积（第1课时）-6.2.4向量的数量积（第一课时）课件【公众号dc008免费分享】.pptxVIP免费

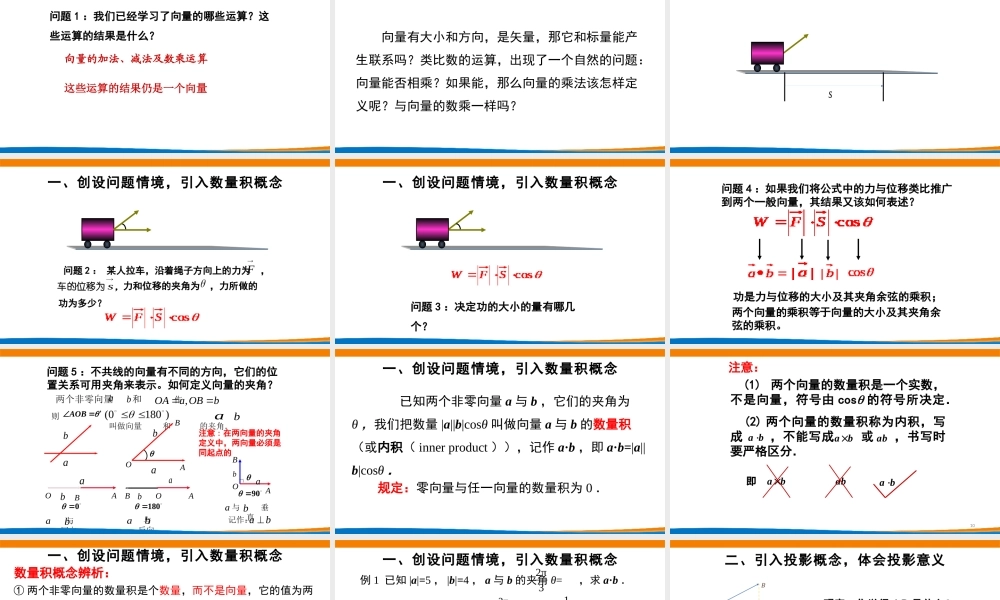
（第一课时）主讲人：深圳市宝安中学（集团）丁俊尹深圳市新课程新教材高中数学在线教学6.2.4向量的数量积问题1：我们已经学习了向量的哪些运算？这些运算的结果是什么？向量的加法、减法及数乘运算复习旧知温故知新这些运算的结果仍是一个向量向量有大小和方向，是矢量，那它和标量能产生联系吗？类比数的运算，出现了一个自然的问题：向量能否相乘？如果能，那么向量的乘法该怎样定义呢？与向量的数乘一样吗？一、创设问题情境，引入数量积概念一、创设问题情境，引入数量积概念s问题2：某人拉车，沿着绳子方向上的力为，车的位移为，力和位移的夹角为，力所做的功为多少？Fs一、创设问题情境，引入数量积概念问题3：决定功的大小的量有哪几个？一、创设问题情境，引入数量积概念问题4：如果我们将公式中的力与位移类比推广到两个一般向量，其结果又该如何表述？两个向量的乘积等于向量的大小及其夹角余弦的乘积。功是力与位移的大小及其夹角余弦的乘积；180与反向abOABab0与同向abOABabb)1800(两个非零向量和，作，ab,OAaOBb�AOBab则叫做向量和的夹角．记作：ab90与垂直abOABab注意:在两向量的夹角定义中，两向量必须是同起点的问题5：不共线的向量有不同的方向，它们的位置关系可用夹角来表示。如何定义向量的夹角？OABbaa已知两个非零向量a与b，它们的夹角为θ，我们把数量|a||b|cosθ叫做向量a与b的数量积（或内积（innerproduct）），记作a·b，即a·b=|a||b|cosθ．规定：零向量与任一向量的数量积为0．一、创设问题情境，引入数量积概念10注意：(1)两个向量的数量积是一个实数，不是向量，符号由cos的符号所决定．(2)两个向量的数量积称为内积，写成，不能写成或，书写时要严格区分．abababab即abab①两个非零向量的数量积是个数量，而不是向量，它的值为两向量的模与两向量夹角的余弦的乘积；②零向量与任一向量的数量积为0，即a·0=0；③符号“·”在向量运算中不是乘号，既不能省略，也不能用“×”代替；④当0≤θ＜时，cosθ＞0，从而a·b>0；当＜θ≤π时，cosθ<0，从而a·b<0．数量积概念辨析：π2π2一、创设问题情境，引入数量积概念例1已知|a|=5，|b|=4，a与b的夹角θ=，求a·b．2π3解：a·b=|a||b|cosθ=5×4×=5×4×(-)=-10．2πcos312例2设|a|=12，|b|=9，a·b=-54，求a与b的夹角...