课时3204_5.2.1三角函数的概念（第一课时）-5.2.1 三角函数的概念（第1课时）【公众号dc008免费分享】.pptxVIP免费

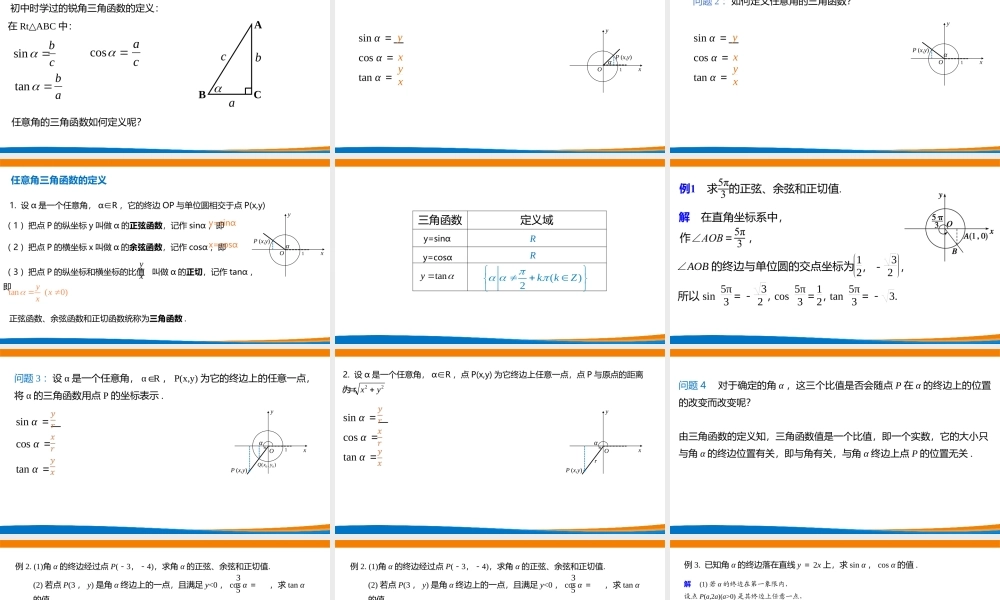
（第一课时）主讲人：深圳高级中学何永丽深圳市新课程新教材高中数学在线教学5.2.1三角函数的概念初中时学过的锐角三角函数的定义：sinbacACB在RtABC△中：costancbcaab任意角的三角函数如何定义呢？知识回顾问题1：锐角α的三角函数值可以用P点的坐标表示吗？αOxyP(x,y)1sinα＝cosα＝tanα＝yxyx问题2：如何定义任意角的三角函数？αOxyP(x,y)1sinα＝cosα＝tanα＝yxyx1.设α是一个任意角，α∈R，它的终边OP与单位圆相交于点P(x,y)（1）把点P的纵坐标y叫做α的正弦函数，记作sinα，即（2）把点P的横坐标x叫做α的余弦函数，记作cosα，即正弦函数、余弦函数和正切函数统称为三角函数.任意角三角函数的定义y=sinαx=cosα（3）把点P的纵坐标和横坐标的比值叫做α的正切，记作tanα，即yxtan(0)yxxαOxyP(x,y)1三角函数定义域()2kkZy=sinαy=cosαtanyRR解在直角坐标系中，∠AOB的终边与单位圆的交点坐标为12，－32，所以sin5π3＝－32，cos5π3＝12，tan5π3＝－3.Oxyα问题3：设α是一个任意角，αR∈，P(x,y)为它的终边上的任意一点，将α的三角函数用点P的坐标表示.100(,)QxyP(x,y).cosα＝sinα＝tanα＝2.设α是一个任意角，α∈R，点P(x,y)为它终边上任意一点，点P与原点的距离为r,OxyαP(x,y).r22rxysinα＝cosα＝tanα＝问题4对于确定的角α，这三个比值是否会随点P在α的终边上的位置的改变而改变呢？由三角函数的定义知，三角函数值是一个比值，即一个实数，它的大小只与角α的终边位置有关，即与角有关，与角α终边上点P的位置无关.OxyαP(-3,-4).例2.(1)角α的终边经过点P(－3，－4)，求角α的正弦、余弦和正切值.解(1)由已知可得r=|OP|＝－32＋－42＝5.于是，sinα＝𝑦𝑟＝－45；cosα＝𝑥𝑟＝－35；tanα＝yx＝43.(2)若点P(3，y)是角α终边上的一点，且满足y<0，cosα＝，求tanα的值.35OxyαP(3,y).例2.(1)角α的终边经过点P(－3，－4)，求角α的正弦、余弦和正切值.(2)若点P(3，y)是角α终边上的一点，且满足y<0，cosα＝，求tanα的值.35解(2) cosα＝332＋y2＝35，∴32＋y2＝5，∴y2＝16， y<0，∴y＝－4，∴tanα＝－43.例3.已知角α的终边落在直线y＝2x上，求sinα，cosα的值.解(1)若α的终边在第一象限内，设点P(a,2a)(a>0)是其终边上任意一点，因为r＝|OP|＝a2＋4a2＝5a所以sinα＝yr＝2a5a＝255，cosα＝xr＝a5a＝55.(2)若α的终边...