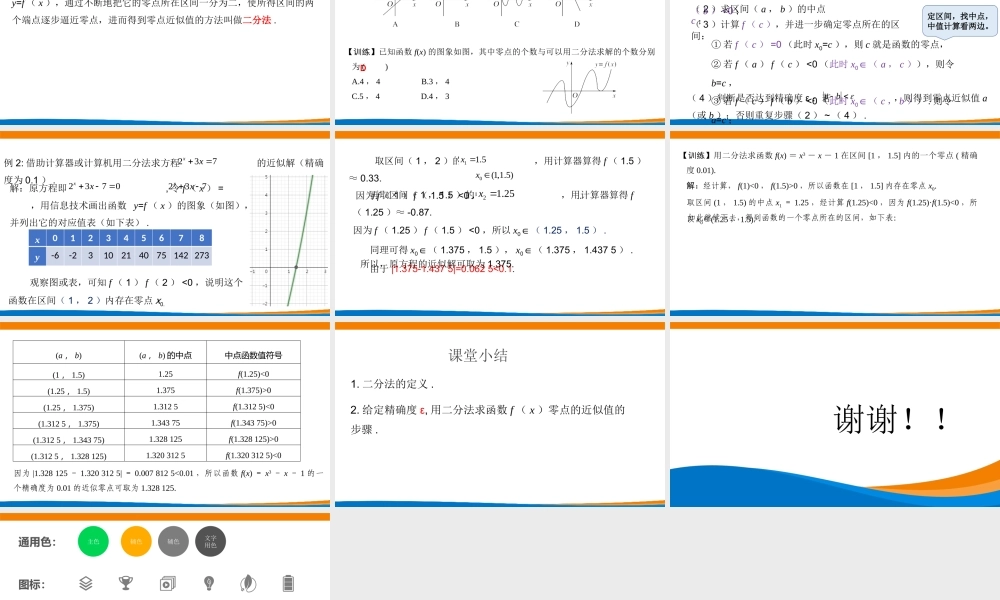
主讲人:深圳第二外国语学校任立勇深圳市新课程新教材高中数学在线教学4.5.2用二分法求方程的近似解函数零点存在性原理一、复习如果函数()yfx在区间,ab上的图象是连续不断的一条曲线,并且有()()0fafb,那么,函数()yfx在区间,ab内有零点,即存在,cab,使得()0fc,这个c也就是方程()0fx的根。如果函数y=f(x)在[a,b]上,图象是连续的,并且在闭区间的两个端点上的函数值符号互异即f(a)f(b)0,﹤且是单调函数,那么这个函数在(a,b)内必有唯一的一个零点.探究一在一个风雨交加的夜里,从某水库闸房到防洪指挥部的电话线路发生了故障,这是一条10km长的路线,如果沿着线路一小段一小段查找,困难很多.每查一个点要爬一次电线杆子,10km长的线路大约有200多根电线杆子.如图,设水库闸房和指挥部分别是A,B;AB首先从中点C开始检查,用随身携带的仪器向两端发射信号进行测试,若发现AC正常,断定故障在BC段;C再取BC的中点D,若发现BD正常,断定故障在CD段;D依次下去,可以把待检查的路线减半。探究一问题1:上述情景中,工人师傅是通过什么方法缩小故障范围的?问题2:如果把故障可能发生的范围缩小在200m左右,至多需要爬几次电线杆子?取中间、减半。6次探究二能否求出方程lnx+2x-6=0的近似解?注:大多数方程都不能像一元二次方程那样用公式求精确解,在实际问题中,往往只需要求出满足一定精度的近似解。探究:用二分法探求方程的近似解(1)函数在区间(2,3)内有零点;()ln26fxxx(2)如果能够将零点所在的范围尽量缩小,那么在一定精确度的要求下,我们可以得到零点的近似值;(3)通过“取中点”的方法逐步缩小零点所在的范围;(4)取区间(2,3)的中点2.5,用计算器算得f(2.5)≈-0.084,因为f(2.5)f(3)<0,所以零点在区间(2.5,3)内;再取区间(2.5,3)的中点2.75,用计算器算得f(2.75)≈0.512,因为f(2.5)f(2.75)<0,所以零点在区间(2.5,2.75)内.(5)由于(2,3)(2.5,3)(2.5,2.75),所以零点所在的范围变小了如果重复上述步骤,那么零点所在的范围会越来越小(如下表).零点所在区间中点的值中点函数近似值(2,3)2.5-0.084(2.5,3)2.750.512(2.5,2.75)2.6250.215(2.5,2.625)2.56250.066(2.5,2.5625)2.53125-0.009(2.53125,2.5625)2.5468750.029(2.53125,2.546875)2.53906250.010(2.53125,2.5390625)2.535156250.001(6)例如,当精确度为0.01时,由于=0.0078125<0.01...