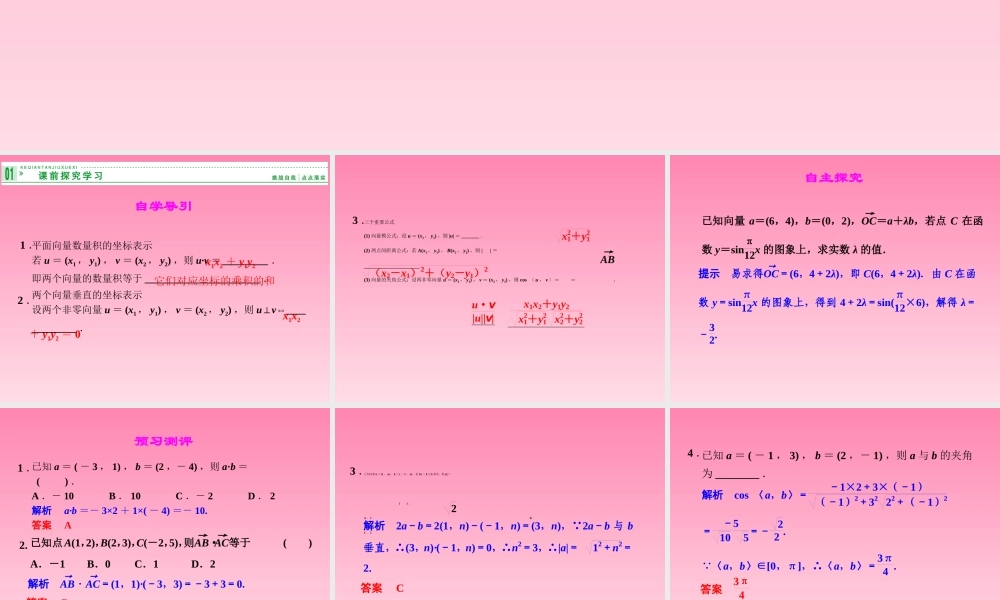
1.理解掌握向量数量积的坐标表达式,会利用坐标进行数量积的运算.2.掌握向量的模、夹角等公式,能根据公式解决向量的模、夹角、垂直等有关问题.4.5.3利用坐标计算数量积平面向量数量积的坐标表示若u=(x1,y1),v=(x2,y2),则u·v=_________.即两个向量的数量积等于_______________________.两个向量垂直的坐标表示设两个非零向量u=(x1,y1),v=(x2,y2),则u⊥v⇔_____________.自学导引1.2.x1x2+y1y2它们对应坐标的乘积的和x1x2+y1y2=0三个重要公式(1)向量模公式:设u=(x1,y1),则|u|=_______.(2)两点间距离公式:若A(x1,y1),B(x2,y2),则||=______________________.(3)向量的夹角公式:设两非零向量u=(x1,y1),v=(x2,y2),则cos〈u,v〉==.3.x21+y21AB→(x2-x1)2+(y2-y1)2u·v|u||v|x1x2+y1y2x21+y21x22+y22自主探究已知向量a=(6,4),b=(0,2),OC→=a+λb,若点C在函数y=sinπ12x的图象上,求实数λ的值.提示易求得OC→=(6,4+2λ),即C(6,4+2λ).由C在函数y=sinπ12x的图象上,得到4+2λ=sin(π12×6),解得λ=-32.已知a=(-3,1),b=(2,-4),则a·b=().A.-10B.10C.-2D.2解析a·b=-3×2+1×(-4)=-10.答案A预习测评1.2.已知点A(1,2),B(2,3),C(-2,5),则AB→·AC→等于().A.-1B.0C.1D.2解析AB→·AC→=(1,1)·(-3,3)=-3+3=0.答案B已知向量a=(1,n),b=(-1,n),若2a-b与b垂直,则|a|=().A.1B.C.2D.43.2解析2a-b=2(1,n)-(-1,n)=(3,n), 2a-b与b垂直,∴(3,n)·(-1,n)=0,∴n2=3,∴|a|=12+n2=2.答案C已知a=(-1,3),b=(2,-1),则a与b的夹角为________.4.解析cos〈a,b〉=-1×2+3×(-1)(-1)2+3222+(-1)2=-5105=-22. 〈a,b〉∈[0,π],∴〈a,b〉=3π4.答案3π4向量的坐标运算与向量运算的区别与联系已知a=(x1,y1),b=(x2,y2),a与b的夹角为θ,则有:名师点睛续表应用数量积运算可以解决两向量的垂直、平行、夹角以及长度等几何问题,在学习中要不断地提高利用向量工具解决数学问题的能力.已知向量a=(3,-1),b=(1,-2),求:(1)a·b;(2)(a+b)2;(3)(a+b)·(a-b).解(1) a=(3,-1),b=(1,-2),∴a·b=3×1+(-1)×(-2)=3+2=5.(2)a+b=(3,-1)+(1,-2)=(4,-3),∴(a+b)2=|a+b|2=42+(-3)2=25.(3)法一 a=(3,-1),b=(1,-2),∴a2=32...