1221高一【数学(人教B版)】平面向量的坐标及其运算(1)-课件.pptxVIP免费

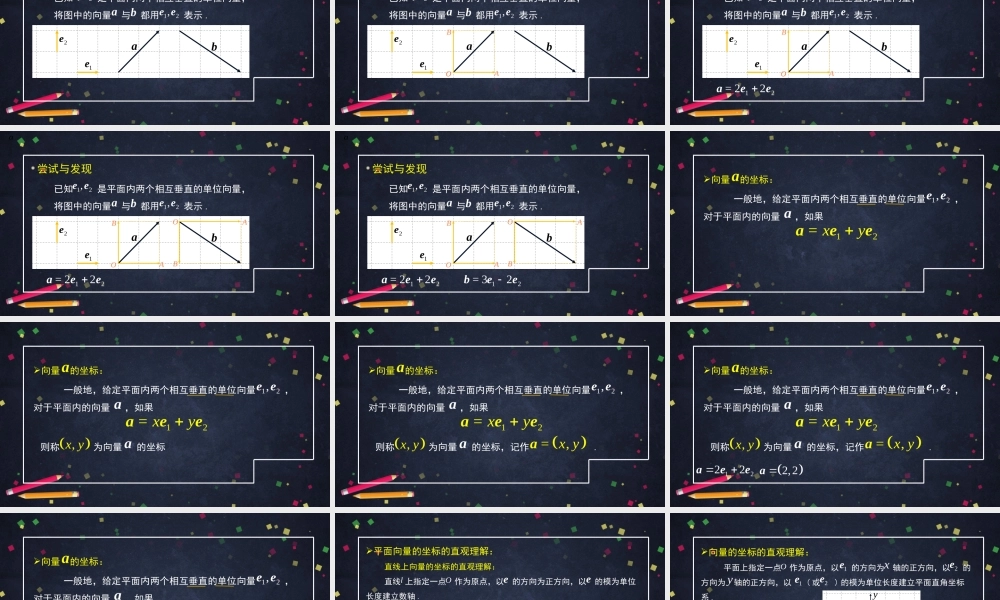
平面向量的坐标及其运算（1）高一年级数学主讲人徐丽北京市第一六一中学北京市中小学空中课堂知识概要一、平面向量的坐标及其求法二、平面向量的相等和运算与坐标的关系三、平面向量的模与坐标的关系四、课堂小结定理共线向量基本定理平面向量基本定理条件给定一个非零向量给定两个不共线的向量结论对任意与共线的向量，则存在唯一的实数，使得对平面内任意向量，存在唯一的实数对，使得本质一、复习回顾aaba,bbac(,)xyxycab一一对应b,xy一一对应c直线上向量的坐标平面向量的坐标基（底）向量二、课堂导入exO1x一一对应bxbe二、课堂导入exO1x一一对应b1e2e直线上向量的坐标平面向量的坐标基（底）向量xbe三、新课讲解1.平面向量的坐标垂直：平面上两个非零向量与，如果它们所在的直线互相垂直，我们就称向量与垂直.abab1e2e三、新课讲解1.平面向量的坐标垂直：平面上两个非零向量与，如果它们所在的直线互相垂直，我们就称向量与垂直.记作.ababab1e2e三、新课讲解1.平面向量的坐标垂直：平面上两个非零向量与，如果它们所在的直线互相垂直，我们就称向量与垂直.记作.规定：零向量与任意向量都垂直.ababab1e2e正交基底：如果平面向量的基底中，，就称这组基底为正交基底.12,ee12ee正交基底：如果平面向量的基底中，，就称这组基底为正交基底.正交分解：在正交基底下向量的分解称为向量的正交分解.12,ee12ee尝试与发现已知是平面内两个相互垂直的单位向量，将图中的向量与都用表示.ab12,ee12,eea1e2eab尝试与发现a1e2eab已知是平面内两个相互垂直的单位向量，将图中的向量与都用表示.ab12,ee12,eeOABO尝试与发现a已知是平面内两个相互垂直的单位向量，将图中的向量与都用表示.ab12,ee12,ee1e2eabOABO12=22aee尝试与发现a已知是平面内两个相互垂直的单位向量，将图中的向量与都用表示.ab12,ee12,ee1e2eabOABABO12=22aee尝试与发现12=22aeea12=32bee1e2eab已知是平面内两个相互垂直的单位向量，将图中的向量与都用表示.ab12,ee12,eeOABABO向量的坐标：一般地，给定平面内两个相互垂直的单位向量，对于平面内的向量，如果12,eea12=xyaeea向量的坐标：一般地，给定平面内两个相互垂直的单位向量，对于平面内的向量，如果则称为向量的坐标12,eea12=xyaee,xyaa向量的坐标：一般地，给定平面内两个相互垂直的单位向量，对于平面内的向量，...