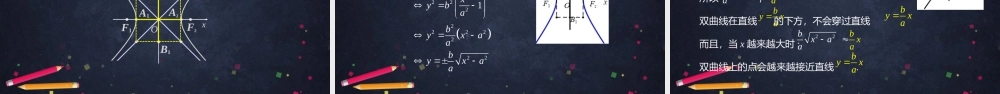1028高二【数学（人教B版）38】双曲线的几何性质-课件.pptxVIP免费

双曲线的几何性质高二年级数学主讲人陈龙清北京师范大学第二附属中学北京市中小学空中课堂复习回顾问题1我们是借助什么来研究椭圆的几何性质的？复习回顾借助椭圆的标准方程.问题1我们是借助什么来研究椭圆的几何性质的？复习回顾问题2我们研究椭圆的几何性质涉及到哪些方面？复习回顾范围、对称性、顶点、离心率等.问题2我们研究椭圆的几何性质涉及到哪些方面？复习回顾问题3双曲线的标准方程是什么？复习回顾焦点在y轴上2222100yxabab，2222100xyabab，双曲线的几何性质2222100xyabab，①22221xyab1、如何从方程①得到双曲线的范围？①22222222111xyxyababxaxa或1、如何从方程①得到双曲线的范围？两直线和所夹平面区域的外侧22222222111xyxyababxaxa或xaxayxx=ax=-aA2A1F1F2O1、如何从方程①得到双曲线的范围？2、如何从方程①得到对称性？22221xyab①方程①的解双曲线上点的坐标方程①的解的特征双曲线的性质.xy，xy，若点是双曲线上任意一点，那么点，，也在双曲线上.,xy,xy,xy,yx22221xyab①,Pxy1,Pxy3,Pxy2,Pyx和关于x轴对称，和关于y轴对称，和关于原点O对称，,Pxy1,Pxy3,Pxy2,Pyx3、如何从方程①得到顶点？22221xyab①3、如何从方程①得到顶点？0y0xxaxa1,0,0AaAa2，1,0,0AaAa2，22221xyab①线段A1A2称为双曲线的实轴.A1A2OF2F1yxyxB2B1A2A1F2F1Oxy等轴双曲线OB2B1A2A1F2F1xy22222222222222211yxbaxybabyxaabyxaa22221xyab①A1A2第一象限：当时，所以，双曲线在直线的下方，不会穿过直线而且，当x越来越大时:双曲线上的点会越来越接近直线.22byxaxaaxa222<=xaxx22bxaaabxbyxa22