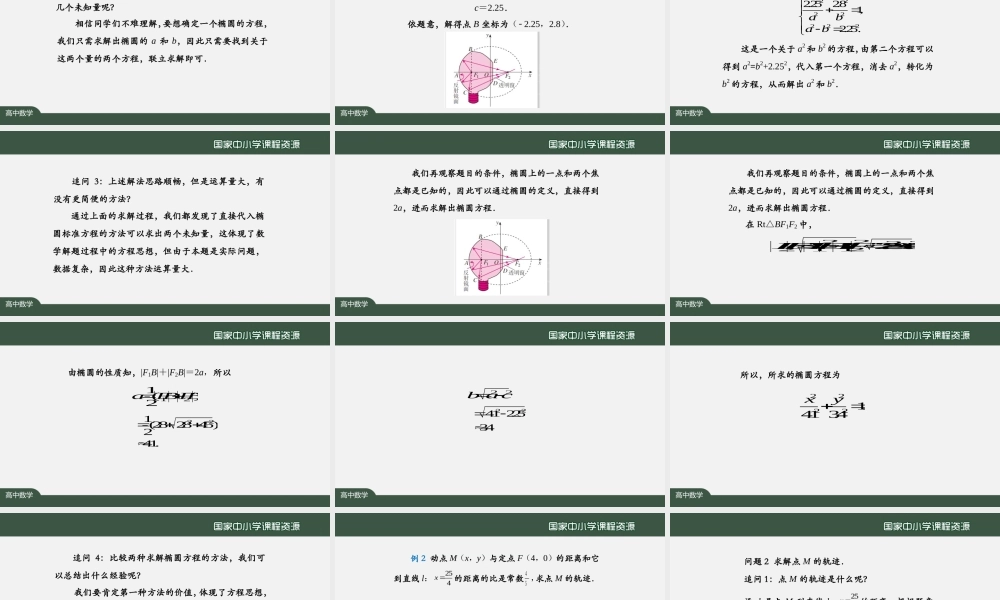
国家中小学课程资源椭圆应用(1)年级:高二学科:数学(人教A版)主讲人:姚未然学校:北京市一七一中学教育集团高中数学温故知新我们首先来一起回顾一下椭圆的概念和它的标准方程.高中数学椭圆的概念:我们把平面内与两个定点F1,F2的距离的和等于常数(大于|F1F2|)的点的轨迹叫做椭圆.这两个定点叫做椭圆的焦点,两焦点间的距离叫做椭圆的焦距,焦距的一半称为半焦距.高中数学椭圆的标准方程:(a>b>0)标准方程22221xyab22221yxab图形高中数学新课讲授前面我们学习了椭圆的定义、标准方程和简单的几何性质,这节课我们综合运用它们和坐标法来解决一些现实问题和数学问题.高中数学例1如图,一种电影放映灯的反射镜面是旋转椭圆面(椭圆绕其对称轴旋转一周形成的曲面)的一部分.过对称轴的截口BAC是椭圆的一部分,灯丝位于椭圆的一个焦点F1上,片门位于另一个焦点F2上.高中数学由椭圆一个焦点F1发出的光线,经过旋转椭圆面反射后集中到另一个焦点F2.已知BC⊥F1F2,|F1B|=2.8cm,|F1F2|=4.5cm.试建立适当的坐标系,求截口BAC所在椭圆的方程(精确到0.1cm).高中数学问题1我们该如何求解截口BAC所在椭圆的方程(精确到0.1cm)呢?追问1:要求解一个实际问题,我们需要做什么呢?高中数学数学抽象实际问题数学模型运算推理数学模型的解解释说明实际问题的解我们可以参照下图的模式通过构建数学模型求解.高中数学将截口BAC所在椭圆的方程设为22221(0).xyabab高中数学追问2:要得到一个椭圆的方程,我们需要求解几个未知量呢?相信同学们不难理解,要想确定一个椭圆的方程,我们只需求解出椭圆的a和b,因此只需要找到关于这两个量的两个方程,联立求解即可.高中数学由椭圆的定义可知,|F1F2|=2c,所以c=2.25.依题意,解得点B坐标为(2.25,2.8).高中数学所以我们可以得到关于a和b的两个方程:22222222.252.81,2.25.abab这是一个关于a2和b2的方程,由第二个方程可以得到a2=b2+2.252,代入第一个方程,消去a2,转化为b2的方程,从而解出a2和b2.高中数学追问3:上述解法思路顺畅,但是运算量大,有没有更简便的方法?通过上面的求解过程,我们都发现了直接代入椭圆标准方程的方法可以求出两个未知量,这体现了数学解题过程中的方程思想,但由于本题是实际问题,数据复杂,因此这种方法运算量大.高中数学我们再观察题目的条件,椭圆上的一点和两个焦点都是已知的,因此可以通过椭圆的定义,...