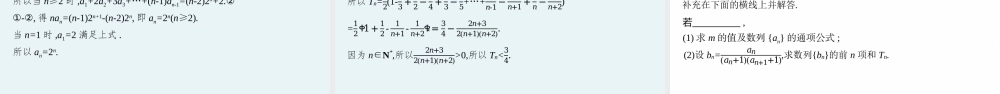高考总复习优化设计GAOKAOZONGFUXIYOUHUASHEJI专项突破三•数列解答题专题三2022突破求数列的通项及前n项和必备知识精要梳理•1.分组转化法具有下列特点的数列常用分组转化法求和:(1)an=bn±cn,且{bn},{cn}为等差数列或等比数列,可采用分组转化法求和.(2)an=且{bn},{cn}为等差数列或等比数列,可采用分组转化法求和.ቊ𝑏𝑛,𝑛为奇数,𝑐𝑛,𝑛为偶数,2.错位相减法一般地,数列{an}是等差数列,{bn}是等比数列,求数列{an·bn}的前n项和时,可采用错位相减法,一般是和式两边同乘等比数列{bn}的公比,然后作差求解.3.裂项相消法实质是将数列的通项分解为两项之差,求和时能消去中间的一些项,最终达到求和的目的,其解题的关键是准确地裂项和消项.(1)裂项原则:一般是前边裂几项,后边就裂几项,直到发现被消去项的规律为止.(2)消项规律:消项后前边剩几项,后边就剩几项,前边剩第几项,后边就剩倒数第几项.关键能力学案突破•考向一分组转化法求和[例1](2021·广东广州模拟)已知数列{an}的前n项和Sn=3𝑛2-𝑛2,数列{log3bn}是公差为-1的等差数列,b1=1.(1)求数列{an},{bn}的通项公式;(2)设cn=a2n+1+b2n+1,求数列{cn}的前n项和Tn.解(1)因为Sn=3𝑛2-𝑛2,所以当n=1时,a1=S1=3-12=1,当n≥2时,an=Sn-Sn-1=3𝑛2-𝑛2−3(𝑛-1)2-(𝑛-1)2=3n-2.又a1=1符合上式,所以an=3n-2.由题意可知log3bn=log3b1+(n-1)×(-1)=1-n,所以bn=31-n.(2)因为cn=a2n+1+b2n+1=3(2n+1)-2+31-(2n+1)=6n+1+19𝑛,所以Tn=𝑛(7+6𝑛+1)2+191-ቀ19ቁ𝑛൨1-19=3n2+4n+18ቀ1-19𝑛ቁ.解题心得分组转化法求和的技巧(1)若能把一个较为复杂的数列的通项分成两(或多)部分,而每一部分对应的前n项和可求,则分别求和相加即可.(2)若一个数列的前n项和不好求,而数列相邻的两项或多项的和相等且为常数,则对该数列先作并项处理,即先合并项,再求和.精典对练·得高分(2021·山东聊城一中一模)已知等差数列{an}的首项为2,前n项和为Sn,正项等比数列{bn}的首项为1,且满足a3=2b2,S5=b2+b4.(1)求数列{an},{bn}的通项公式;(2)设cn=(-1)nlog3Sn+log3bn,求数列{cn}的前26项和.解(1)设{an}的公差为d,{bn}的公比为q(q>0).由题意得ቊ𝑎1+2𝑑=2𝑏1𝑞,5𝑎1+5×42𝑑=𝑏1𝑞+𝑏1𝑞3,即൜2+2𝑑=2𝑞,10+10𝑑=𝑞+𝑞3,解得൜𝑑=2,𝑞=3.∴an=2+2(n-1)=2n,bn=1×3n-1=3n-1.(2) Sn=12n(2+2n)=n(n+1),∴cn=(-1)nlog3[n(n+1)]+log33n-1=(-1)nlog3n+(-1)nlog3(n+1)+n-1.设{cn}的前n项和为Tn,则T26=(-log31-log32+0)+(log32+log33+1)+(-log33-log34+2)+…...