湘教版高中数学必修3第6章立体几何初步6.2.3 垂直关系教学课件 (共24张PPT).pptVIP免费

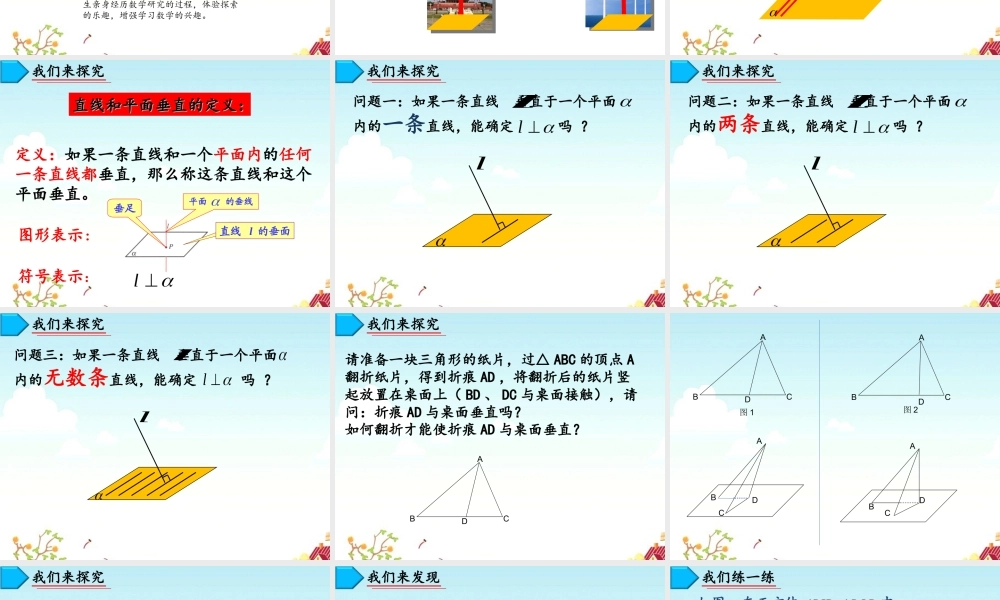
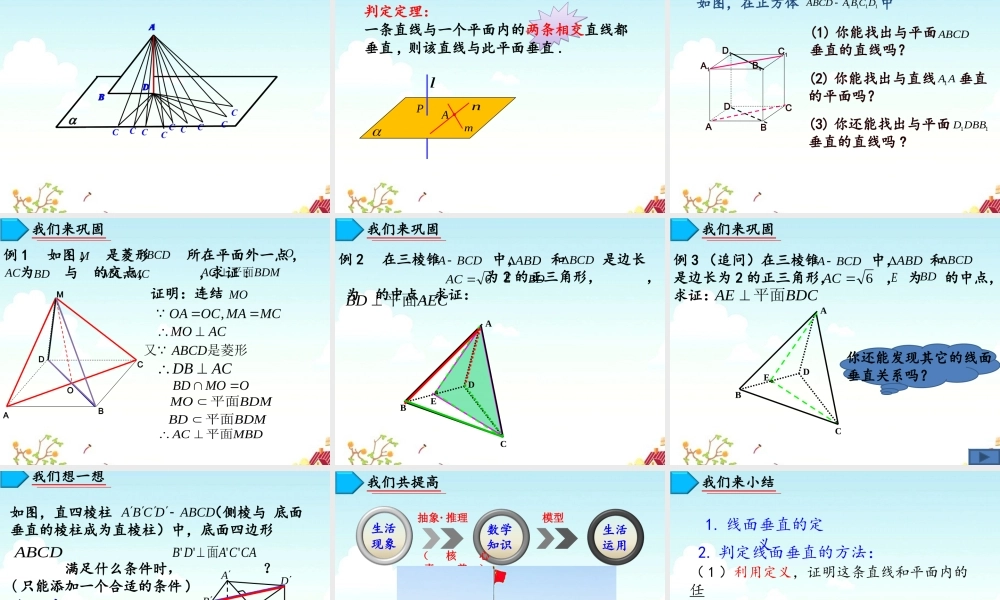
我们来感受Al我们来回顾Bl我们来回顾Bl直线与平面垂直的判定目标LearningTarget知识与技能通过直观感知、操作确认，理解线面垂直的定义，归纳线面垂直的判定定理，并能运用定义和定理证明一些空间位置关系的简单命题。过程与方法通过线面垂直定义及定理的探究过程，感知几何直观能力和抽象概括能力，体会转化思想在解决问题中的运用。情感、态度与价值观通过线面垂直定义及定理的探究，让学生亲身经历数学研究的过程，体验探索的乐趣，增强学习数学的兴趣。【思考】如何定义“直线与平面垂直”？我们来感受垂直l我们再来感受P直线和平面垂直的定义：直线和平面垂直的定义：定义：如果一条直线和一个平面内的任何一条直线都垂直，那么称这条直线和这个平面垂直。符号表示：l图形表示：平面的垂线直线l的垂面垂足我们来探究问题一：如果一条直线垂直于一个平面内的一条直线，能确定吗？我们来探究lll问题二：如果一条直线垂直于一个平面内的两条直线，能确定吗？我们来探究lll问题三：如果一条直线垂直于一个平面内的无数条直线，能确定吗？我们来探究lll请准备一块三角形的纸片，过△ABC的顶点A翻折纸片，得到折痕AD，将翻折后的纸片竖起放置在桌面上（BD、DC与桌面接触），请问：折痕AD与桌面垂直吗？ABDC如何翻折才能使折痕AD与桌面垂直？我们来探究ABDCABCDABDCABCD图1图2ABC我们来探究D判定定理：一条直线与一个平面内的两条相交直线都垂直,则该直线与此平面垂直.lAnm我们来发现PABCDA1B1C1D1如图，在正方体中(1)你能找出与平面垂直的直线吗？(2)你能找出与直线垂直的平面吗？(3)你还能找出与平面垂直的直线吗?我们练一练1111DCBAABCDABCDAA111DBBD例1如图,是菱形所在平面外一点,为与的交点，,求证:证明：MABCDO连结我们来巩固MCMAOCOA,ACMO是菱形又ABCDACDBBDMMO平面BDMBD平面MBDAC平面MOMABCDOACBDMCMABDMAC平面BDMOOABCDE例2在三棱锥中，和是边长为2的正三角形，，为的中点,求证：BCDAABDBCD6ACEBDAECBD平面我们来巩固ABCDE例3（追问）在三棱锥中，和是边长为2的正三角形，，为的中点，求证：BCDAABDBCD6ACEBDBDCAE平面你还能发现其它的线面垂直关系吗？我们来巩固如图，直四棱柱（侧棱与底面垂直的棱柱成为直棱柱）中，底面四边形满足什么条件时，？(只能添加一个合适的条件)ABCDDCBAAABBCCDD解:底面ABCD可以是菱形,正...