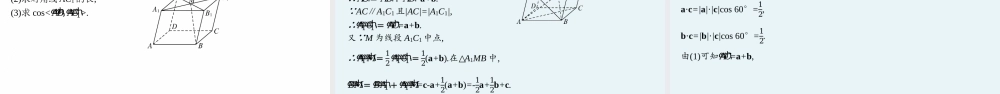高中同步学案优化设计GAOZHONGTONGBUXUEANYOUHAUSHEJI3.1空间向量基本定理第三章2021内容索引0102课前篇自主预习课堂篇探究学习核心素养思维脉络1.掌握空间向量基本定理.(数学抽象)2.会用空间向量基本定理解决有关问题.(逻辑推理)课前篇自主预习激趣诱思在平面内,任意给定两个不共线的向量a,b,根据平面向量基本定理,对于该平面内的任意一个向量p,存在唯一的有序实数对(x,y),使得p=xa+yb.设a,b,c是空间三个不共面的向量,p是空间任意一个向量,是否可以用向量a,b,c来表示向量p?知识点拨空间向量基本定理空间向量基本定理:如果向量a,b,c是空间三个不共面的向量,p是空间任意一个向量,那么存在唯一的三元有序实数组(x,y,z),使得p=xa+yb+zc.由上述定理可知,如果向量a,b,c是空间三个不共面向量,那么所有的空间向量组成的集合就是{p|p=xa+yb+zc,x,y,z∈R},这个集合可以看成是由向量a,b,c生成的,这时{a,b,c}叫作空间的一组基,其中a,b,c都叫作基向量.名师点析由于零向量与任意一个非零向量共线,与任意两个不共线的非零向量共面,所以若三个向量不共面,就说明它们都不是零向量.微练习在三棱柱ABC-A1B1C1中,可以作为空间向量一组基的是()A.𝐴𝐵ሬሬሬሬሬԦ,𝐵𝐶ሬሬሬሬሬԦ,𝐴1𝐶1ሬሬሬሬሬሬሬሬሬԦB.𝐴𝐵ሬሬሬሬሬԦ,𝐴𝐵1ሬሬሬሬሬሬሬԦ,𝐴𝐴1ሬሬሬሬሬሬሬԦC.𝐴𝐵ሬሬሬሬሬԦ,𝐴𝐶ሬሬሬሬሬԦ,𝐴𝐴1ሬሬሬሬሬሬሬԦD.𝐴𝐴1ሬሬሬሬሬሬሬԦ,𝐴𝐶ሬሬሬሬሬԦ,𝐴1𝐶1ሬሬሬሬሬሬሬሬሬԦ答案C解析只有不共面的三个向量才能作为一组基,在三棱柱中,不共面,可作为基.𝐴𝐵ሬሬሬሬሬԦ,𝐴𝐶ሬሬሬሬሬԦ,𝐴𝐴1ሬሬሬሬሬሬሬԦ课堂篇探究学习探究一基的判断例1(1)设x=a+b,y=b+c,z=c+a,且{a,b,c}是空间的一组基,给出下列向量组:①{a,b,x},②{x,y,z},③{b,c,z},④{x,y,a+b+c}.其中可以作为空间一组基的向量组有()A.1个B.2个C.3个D.4个答案C解析如图所示,令a=𝐴𝐵ሬሬሬሬሬԦ,b=𝐴𝐴1ሬሬሬሬሬሬሬԦ,c=𝐴𝐷ሬሬሬሬሬԦ,则x=𝐴𝐵1ሬሬሬሬሬሬሬԦ,y=𝐴𝐷1ሬሬሬሬሬሬሬԦ,z=𝐴𝐶ሬሬሬሬሬԦ,a+b+c=𝐴𝐶1ሬሬሬሬሬሬሬԦ.由于A,B1,C,D1四点不共面,可知向量x,y,z也不共面,同理b,c,z和x,y,a+b+c也不共面,故选C.(2)已知{e1,e2,e3}是空间的一组基,且𝑂𝐴ሬሬሬሬሬԦ=e1+2e2-e3,𝑂𝐵ሬሬሬሬሬԦ=-3e1+e2+2e3,𝑂𝐶ሬሬሬሬሬԦ=e1+e2-e3,试判断{𝑂𝐴ሬሬሬሬሬԦ,𝑂𝐵ሬሬሬሬሬԦ,𝑂𝐶ሬሬሬሬሬԦ}能否作为空间的一组基.解设𝑂𝐴ሬሬሬሬሬԦ=x𝑂𝐵...