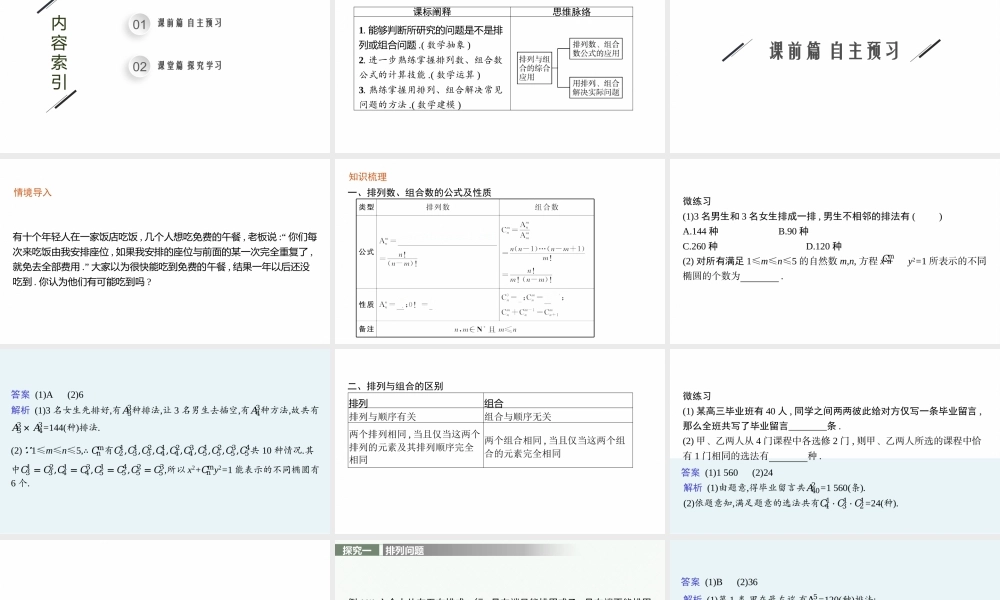
高中同步学案优化设计GAOZHONGTONGBUXUEANYOUHAUSHEJI习题课——排列与组合的综合应用第六章2021内容索引0102课前篇自主预习课堂篇探究学习课标阐释思维脉络1.能够判断所研究的问题是不是排列或组合问题.(数学抽象)2.进一步熟练掌握排列数、组合数公式的计算技能.(数学运算)3.熟练掌握用排列、组合解决常见问题的方法.(数学建模)课前篇自主预习情境导入有十个年轻人在一家饭店吃饭,几个人想吃免费的午餐,老板说:“你们每次来吃饭由我安排座位,如果我安排的座位与前面的某一次完全重复了,就免去全部费用.”大家以为很快能吃到免费的午餐,结果一年以后还没吃到.你认为他们有可能吃到吗?知识梳理一、排列数、组合数的公式及性质微练习(1)3名男生和3名女生排成一排,男生不相邻的排法有()A.144种B.90种C.260种D.120种(2)对所有满足1≤m≤n≤5的自然数m,n,方程x2+y2=1所表示的不同椭圆的个数为.𝐶nm答案(1)A(2)6解析(1)3名女生先排好,有𝐴33种排法,让3名男生去插空,有𝐴43种方法,故共有𝐴33×𝐴43=144(种)排法.(2) 1≤m≤n≤5,∴𝐶nm有𝐶21,𝐶31,𝐶32,𝐶41,𝐶42,𝐶43,𝐶51,𝐶52,𝐶53,𝐶54共10种情况.其中𝐶31=𝐶32,𝐶41=𝐶43,𝐶51=𝐶54,𝐶52=𝐶53,所以x2+𝐶nmy2=1能表示的不同椭圆有6个.二、排列与组合的区别排列组合排列与顺序有关组合与顺序无关两个排列相同,当且仅当这两个排列的元素及其排列顺序完全相同两个组合相同,当且仅当这两个组合的元素完全相同微练习(1)某高三毕业班有40人,同学之间两两彼此给对方仅写一条毕业留言,那么全班共写了毕业留言条.(2)甲、乙两人从4门课程中各选修2门,则甲、乙两人所选的课程中恰有1门相同的选法有种.答案(1)1560(2)24解析(1)由题意,得毕业留言共𝐴402=1560(条).(2)依题意知,满足题意的选法共有𝐶41·𝐶31·𝐶21=24(种).课堂篇探究学习探究一排列问题例1(1)六个人从左至右排成一行,最左端只能排甲或乙,最右端不能排甲,则不同的排法共有()A.192种B.216种C.240种D.288种(2)把5件不同产品摆成一排,若产品A与产品B相邻,且产品A与产品C不相邻,则不同的摆法有种.答案(1)B(2)36解析(1)第1类,甲在最左端,有A55=120(种)排法;第2类,乙在最左端,有4×A44=96(种)排法,所以共有120+96=216(种)排法.(2)记其余两种产品为D,E,由于A,B相邻,则视为一个元素,先与D,E排列,有A22A33种方法.再将C插入,仅有3个空位可选,共有A22A33C31=2×6×3=36(种)不同的摆法.反思感悟求解排列问题的六种主要方法直接法把符合条件的排列数直接列式计算...