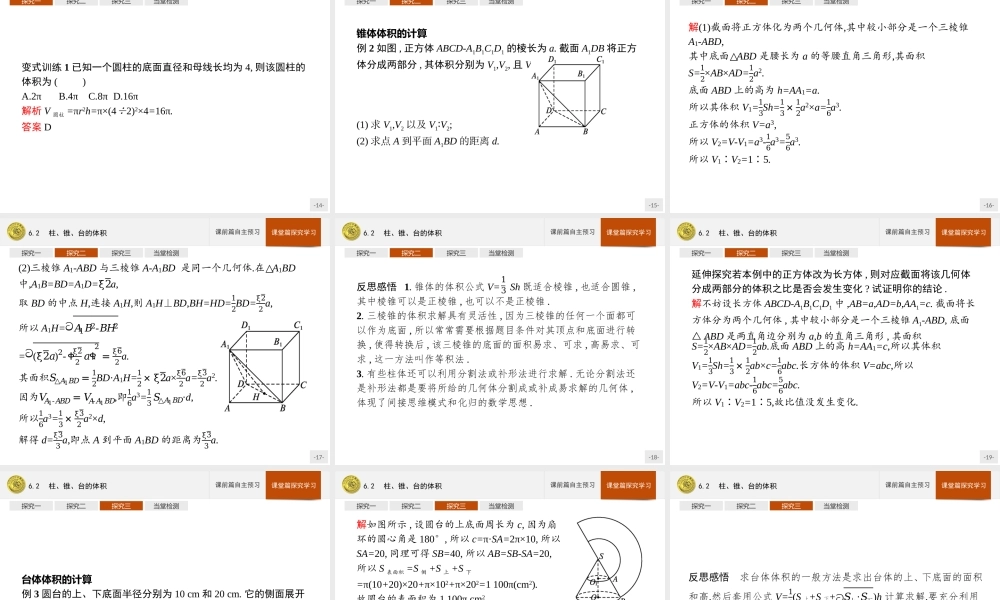
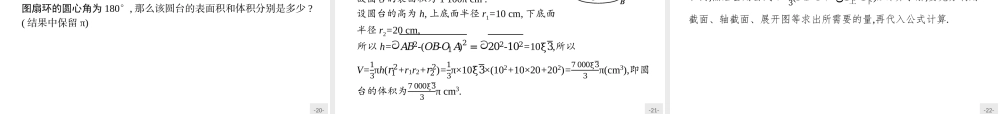-1-6.2柱、锥、台的体积-2-6.2柱、锥、台的体积课前篇自主预习课堂篇探究学习课标阐释1.掌握柱体、锥体、台体的体积计算公式及其三种几何体体积计算公式的内在联系.(逻辑推理)2.会利用柱体、锥体、台体的体积计算公式求有关几何体的体积,并掌握求几何体体积的基本技巧.(数学运算)思维脉络-3-6.2柱、锥、台的体积课前篇自主预习课堂篇探究学习课前篇自主预习激趣诱思知识点拨有一次,爱迪生把一只灯泡交给他的助手阿普顿,让他计算一下这只灯泡的容积是多少.阿普顿是普林斯顿大学数学系高才生,又在德国深造了一年,数学素养相当不错.他拿着这只梨形的灯泡,打量了好半天,又特地找来皮尺,上下量了尺寸,画出了各种示意图,还列出了一道又一道的算式.一个钟头过去了,爱迪生着急了,跑来问他算出来了没有.“正算到一半.”阿普顿慌忙回答,豆大的汗珠从他的额角上滚了下来.爱迪生十分诧异,走近一看,在阿普顿的面前,好几张白纸上写满了密密麻麻的算式.爱迪生微笑着说:“何必这么复杂呢?”阿普顿又重新调整思路,一会儿他飞快地跑进实验室,不到1分钟,没有经过任何运算,就把灯泡的容积准确地求出来了.大家能猜出阿普顿使用的巧妙方法吗?阿普顿的这种处理方法对大家有何帮助?-4-6.2柱、锥、台的体积课前篇自主预习课堂篇探究学习课前篇自主预习激趣诱思知识点拨柱体、锥体、台体的体积公式名称体积(V)公式备注柱体棱柱V=Shh为棱柱的高S为棱柱的底面面积圆柱V=πr2h=Shr为圆柱的底面半径h为圆柱的高S为圆柱的底面面积锥体棱锥V=ShS为棱锥的底面面积h为棱锥的高圆锥r为圆锥的底面半径h为圆锥的高S为圆锥的底面面积13-5-6.2柱、锥、台的体积课前篇自主预习课堂篇探究学习课前篇自主预习激趣诱思知识点拨名称体积(V)公式备注台体棱台S上,S下分别为棱台上、下底面的面积h为棱台的高圆台r,r'分别为圆台上、下底面的半径h为圆台的高,S上,S下分别为圆台上、下底面的面积-6-6.2柱、锥、台的体积课前篇自主预习课堂篇探究学习课前篇自主预习激趣诱思知识点拨名师点析在台体的体积公式中,如果设S上=S下=S,就得到柱体的体积公式V柱体=Sh;如果设S上=0,S下=S,就得到锥体的体积公式V锥体=Sh.因此,柱体、锥体、台体的体积公式之间的关系,可表示为:13由图可见,柱体、锥体的体积公式是台体的体积公式的特例.-7-6.2柱、锥、台的体积课前篇自主预习课堂篇探究学习课前篇自主预习激趣诱思知识点拨微思考1把一张长为6、宽为4的矩形纸片卷成一个圆柱形,使其对边恰好重合,所围圆柱的底面半径是...