高中同步学案优化设计GAOZHONGTONGBUXUEANYOUHAUSHEJI习题课指数函数图象与性质的综合应用第6章2021课堂篇探究学习探究一比较大小例1(1)已知a=ඥ5-12,函数f(x)=ax,若实数m,n满足f(m)>f(n),则m,n的大小关系为.(2)比较下列各题中两个值的大小:①ቀ57ቁ-1.8,ቀ57ቁ-2.5;②ቀ23ቁ-0.5,ቀ34ቁ-0.5;③0.20.3,0.30.2.(1)答案m
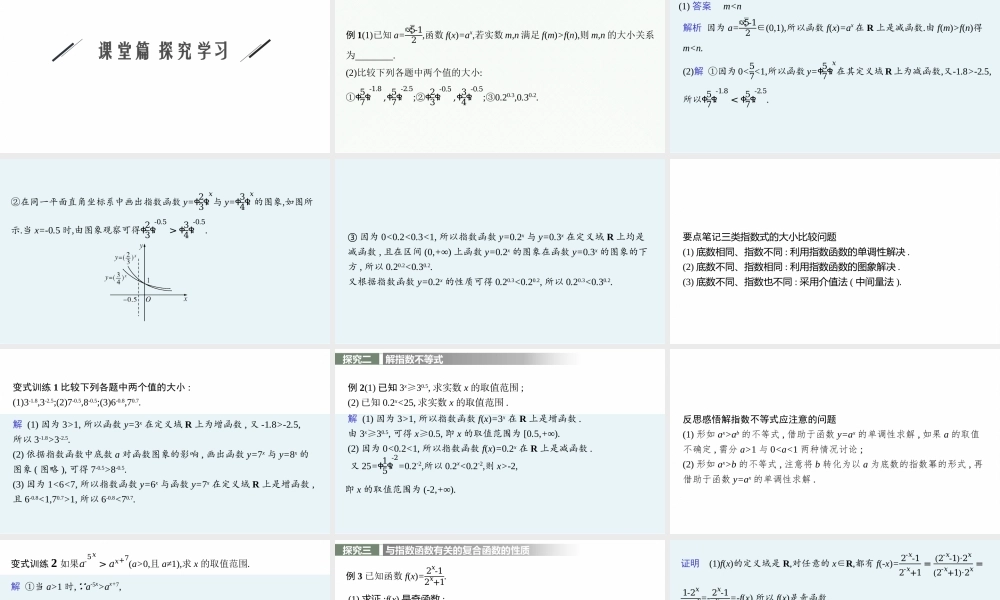
f(n)得m-2.5,所以ቀ57ቁ-1.8<ቀ57ቁ-2.5.②在同一平面直角坐标系中画出指数函数y=ቀ23ቁ𝑥与y=ቀ34ቁ𝑥的图象,如图所示.当x=-0.5时,由图象观察可得ቀ23ቁ-0.5>ቀ34ቁ-0.5.③因为0<0.2<0.3<1,所以指数函数y=0.2x与y=0.3x在定义域R上均是减函数,且在区间(0,+∞)上函数y=0.2x的图象在函数y=0.3x的图象的下方,所以0.20.2<0.30.2.又根据指数函数y=0.2x的性质可得0.20.3<0.20.2,所以0.20.3<0.30.2.要点笔记三类指数式的大小比较问题(1)底数相同、指数不同:利用指数函数的单调性解决.(2)底数不同、指数相同:利用指数函数的图象解决.(3)底数不同、指数也不同:采用介值法(中间量法).变式训练1比较下列各题中两个值的大小:(1)3-1.8,3-2.5;(2)7-0.5,8-0.5;(3)6-0.8,70.7.解(1)因为3>1,所以函数y=3x在定义域R上为增函数,又-1.8>-2.5,所以3-1.8>3-2.5.(2)依据指数函数中底数a对函数图象的影响,画出函数y=7x与y=8x的图象(图略),可得7-0.5>8-0.5.(3)因为1<6<7,所以指数函数y=6x与函数y=7x在定义域R上是增函数,且6-0.8<1,70.7>1,所以6-0.8<70.7.探究二解指数不等式例2(1)已知3x≥30.5,求实数x的取值范围;(2)已知0.2x<25,求实数x的取值范围.解(1)因为3>1,所以指数函数f(x)=3x在R上是增函数.由3x≥30.5,可得x≥0.5,即x的取值范围为[0.5,+∞).(2)因为0<0.2<1,所以指数函数f(x)=0.2x在R上是减函数.又25=ቀ15ቁ-2=0.2-2,所以0.2x<0.2-2,则x>-2,即x的取值范围为(-2,+∞).反思感悟解指数不等式应注意的问题(1)形如ax>ab的不等式,借助于函数y=ax的单调性求解,如果a的取值不确定,需分a>1与0b的不等式,注意将b转化为以a为底数的指数幂的形式,再借助于函数y=ax的单调性求解.变式训练2如果𝑎-5𝑥>𝑎𝑥+7(a>0,且a≠1),求x的取值范围.解①当a>1时, a-5x>ax+7,∴-5x>x+7,解得x<-76.②当0ax+7,∴-5x-76.综上所述,当a>1时,x∈ቀ-∞,-76ቁ;当0