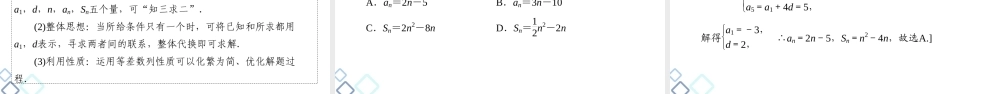第6章 第2节 等差数列及其前n项和.pptVIP免费

第六章数列第二节等差数列及其前n项和1走进教材·夯实基础细研考点·突破题型课后限时集训23第二节等差数列及其前n项和第二节等差数列及其前n项和1走进教材·夯实基础细研考点·突破题型课后限时集训23[考试要求]1.理解等差数列的概念.2.掌握等差数列的通项公式与前n项和公式.3.能在具体的问题情境中识别数列的等差关系，并能用等差数列的有关知识解决相应的问题.4.了解等差数列与一次函数的关系．第二节等差数列及其前n项和1走进教材·夯实基础细研考点·突破题型课后限时集训2301走进教材·夯实基础梳理·必备知识激活·必备技能第二节等差数列及其前n项和1走进教材·夯实基础细研考点·突破题型课后限时集训231．等差数列(1)定义：一般地，如果一个数列从_______起，每一项与它的前一项的___等于___________，那么这个数列就叫做等差数列，这个常数叫做等差数列的_____，公差通常用字母d表示．数学语言表示为_______________(n∈N*)，d为常数．(2)等差中项：数列a，A，b成等差数列的充要条件是_________，其中A叫做a，b的_________．第2项差同一个常数公差an＋1－an＝d等差中项A＝a＋b2第二节等差数列及其前n项和1走进教材·夯实基础细研考点·突破题型课后限时集训232．等差数列的有关公式(1)通项公式：an＝_______________.(2)前n项和公式：Sn＝na1＋nn－12d＝na1＋an2.a1＋(n－1)d第二节等差数列及其前n项和1走进教材·夯实基础细研考点·突破题型课后限时集训233．等差数列的通项公式及前n项和公式与函数的关系(1)当d≠0时，等差数列{an}的通项公式an＝dn＋(a1－d)是关于d的一次函数．(2)当d≠0时，等差数列{an}的前n项和Sn＝d2n2＋a1－d2n是关于n的二次函数．第二节等差数列及其前n项和1走进教材·夯实基础细研考点·突破题型课后限时集训234．等差数列的前n项和的最值在等差数列{an}中，a1>0，d<0，则Sn存在最___值；若a1<0，d>0，则Sn存在最___值．大小第二节等差数列及其前n项和1走进教材·夯实基础细研考点·突破题型课后限时集训23[常用结论]等差数列的常用性质(1)通项公式的推广：an＝am＋(n－m)d(n，m∈N*)．(2)若{an}为等差数列，且m＋n＝p＋q，则am＋an＝ap＋aq(m，n，p，q∈N*)．(3)若{an}是等差数列，公差为d，则ak，ak＋m，ak＋2m，…(k，m∈N*)是公差为md的等差数列．第二节等差数列及其前n项和1走进教材·夯实基础细研考点·突破题型课后限时集训23(4)数列Sm，S2m－Sm，S3m－S2m，…(m∈N*)也是等差...