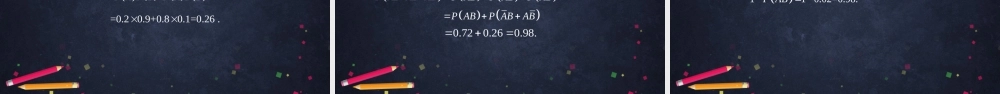1204高一【数学(人教B版)】随机事件的独立性-课件.pptxVIP免费

随机事件的独立性高一年级数学主讲人刘亚洲北京师范大学第二附属中学北京市中小学空中课堂A复习引入事件和事件不同时发生;B互斥事件：A事件和事件不同时发生，且B对立事件：,AB必有一个发生.==ABBA，nmmnABAB引例五一劳动节学校放假三天，甲、乙两名同学都打算去敬老院做志愿者，甲同学准备在三天中随机选择一天，乙同学准备在前两天中随机选一天.记:甲同学选的是第一天，：乙同学选的是第一天.ABnmmn（1）直觉上，你觉得事件发生与否会影响事件发生的概率吗？BA因为两位同学没有提前商量各自做决定，两人哪天去养老院互不影响，所以事件发生与否不影响事件发生的概率.AB（2）分别计算，你有什么发现？PAPBPAB，，（2）分别计算，你有什么发现？解用表示甲选的是第天，乙选的是第天，则(,)ij1,2,3ii=1,2jj{(1,1),(1,2),(2,1),(2,2)(3,1),(3,2)}，，PAPBPAB，，（2）分别计算，你有什么发现？解用表示甲选的是第天，乙选的是第天，则(,)ij1,2,3ii=1,2jj{(1,1),(1,2),(2,1),(2,2)(3,1),(3,2)}，，{(1,1),(1,2)}A，{(1,1),(2,1),(3,1)}B，{(1,1)}AB，111===326PAPBPAB，，，=.PABPAPBPAPBPAB，，两个事件相互独立的定义：对任意两个事件和，如果成立，则称事件和相互独立，简称独立.AB=PABPAPBAB事件和事件相互独立的直观理解是，事件是否发生不影响事件发生的概率，事件是否发生也不影响事件发生的概率.ABAABB思考1分别判断必然事件和不可能事件与事件是否相互独立？AAA，PAPAPPA；A，0.PAPPPA思考2当事件和相互独立，与，与，与是否也相互独立？ABABABAB==,AABBABAB==PAPABBPABAB=PAPBPAB=PABPAB=PABPAPAPB=1PAPB=PAPB例1甲、乙两人各掷一枚均匀的骰子，观察朝上的点数，记：甲得到的点数是2，：乙得到的点数为奇数.（1）求，判断事件与事件是否相互独立；（2）求.ABPAPBPAB，，PABAB解：（1）用表示甲得到的点数是，乙得到的点数是，则.(,)ijij{,,1,2,3,4,5,6}ijij（）111===6212PAPBPAB，，，=PABPAPB，所以事件与事件相互独立.AB（2）求因为事件与事件相互独立，所以和也相互独立.ABAB115===6212PA...