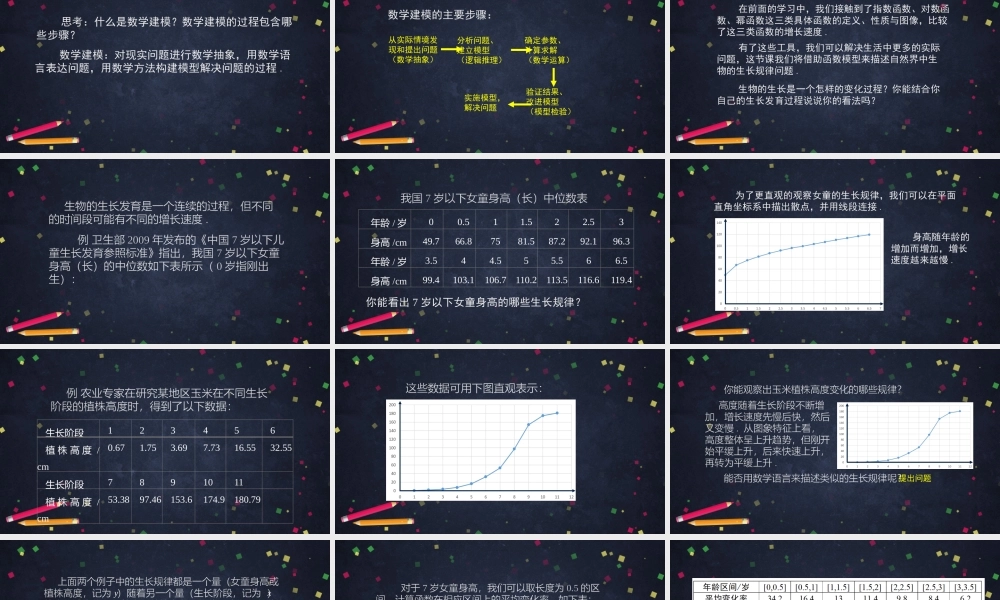
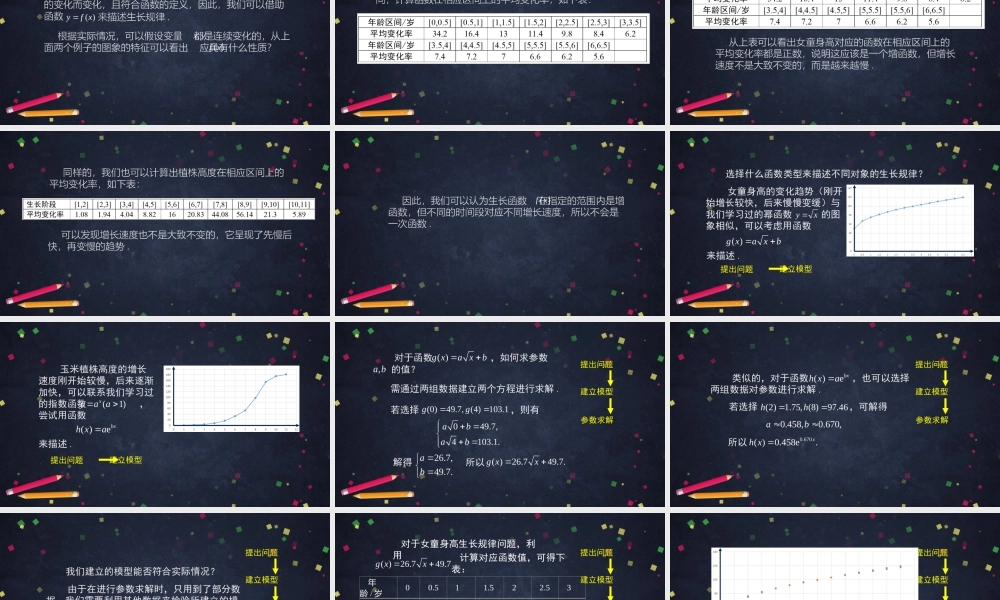
数学建模活动(3)高一年级数学主讲人罗德建北京师范大学附属中学北京市中小学空中课堂思考:什么是数学建模?数学建模的过程包含哪些步骤?数学建模:对现实问题进行数学抽象,用数学语言表达问题,用数学方法构建模型解决问题的过程.数学建模的主要步骤:从实际情境发现和提出问题(数学抽象)分析问题、建立模型(逻辑推理)确定参数、计算求解(数学运算)验证结果、改进模型(模型检验)实施模型,解决问题在前面的学习中,我们接触到了指数函数、对数函数、幂函数这三类具体函数的定义、性质与图像,比较了这三类函数的增长速度.有了这些工具,我们可以解决生活中更多的实际问题,这节课我们将借助函数模型来描述自然界中生物的生长规律问题.生物的生长是一个怎样的变化过程?你能结合你自己的生长发育过程说说你的看法吗?生物的生长发育是一个连续的过程,但不同的时间段可能有不同的增长速度.例卫生部2009年发布的《中国7岁以下儿童生长发育参照标准》指出,我国7岁以下女童身高(长)的中位数如下表所示(0岁指刚出生):年龄/岁00.511.522.53身高/cm49.766.87581.587.292.196.3年龄/岁3.544.555.566.5身高/cm99.4103.1106.7110.2113.5116.6119.4我国7岁以下女童身高(长)中位数表你能看出7岁以下女童身高的哪些生长规律?为了更直观的观察女童的生长规律,我们可以在平面直角坐标系中描出散点,并用线段连接.身高随年龄的增加而增加,增长速度越来越慢.例农业专家在研究某地区玉米在不同生长阶段的植株高度时,得到了以下数据:生长阶段123456植株高度/cm0.671.753.697.7316.5532.55生长阶段7891011植株高度/cm53.3897.46153.6174.9180.79这些数据可用下图直观表示:高度随着生长阶段不断增加,增长速度先慢后快,然后又变慢.从图象特征上看,高度整体呈上升趋势,但刚开始平缓上升,后来快速上升,再转为平缓上升.你能观察出玉米植株高度变化的哪些规律?能否用数学语言来描述类似的生长规律呢?提出问题上面两个例子中的生长规律都是一个量(女童身高或植株高度,记为)随着另一个量(生长阶段,记为)的变化而变化,且符合函数的定义,因此,我们可以借助函数()yfx来描述生长规律.yx根据实际情况,可以假设变量都是连续变化的,从上面两个例子的图象的特征可以看出应具有什么性质?,xy()fx对于7岁女童身高,我们可以取长度为0.5的区间,计算函数在相应区间上的平均变化率,如下表:从上表可以看出女童身高对应的函数在相应区间上...