0925高二【数学（人教B）】坐标法-课件.pptxVIP免费

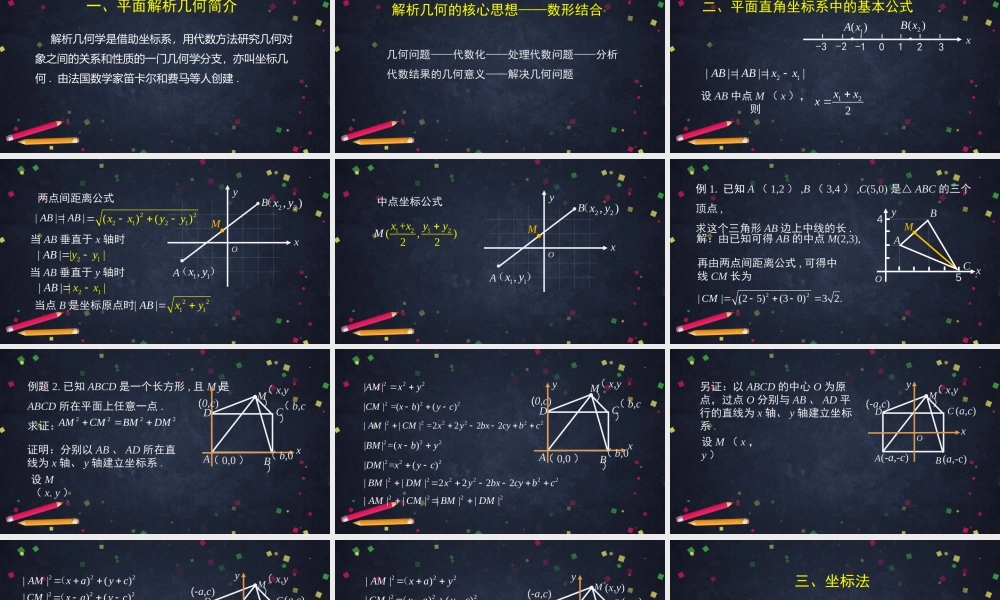
坐标法高二年级数学主讲人李娜北京市第八中学北京市中小学空中课堂解析几何学是借助坐标系，用代数方法研究几何对象之间的关系和性质的一门几何学分支，亦叫坐标几何.由法国数学家笛卡尔和费马等人创建.一、平面解析几何简介解析几何的核心思想——数形结合几何问题——代数化——处理代数问题——分析代数结果的几何意义——解决几何问题二、平面直角坐标系中的基本公式-3-2-10123x1()Ax2()Bx21||||||ABABxx�设AB中点M（x），则122xxx||||ABAB�222121()()xxyy两点间距离公式当AB垂直于x轴时当AB垂直于y轴时当点B是坐标原点时21||||yABy21||||xABx2211||ABxyB22,)xy（A11,xy（）MxyO中点坐标公式1212+(,)22MxxyyB22,)xy（A11,xy（）MxyO例1.已知A（1,2）,B（3,4）,C(5,0)是△ABC的三个顶点,求这个三角形AB边上中线的长.解：由已知可得AB的中点M(2,3),再由两点间距离公式,可得中线CM长为22||(25)(30)32.CMMxO4CBA5y例题2.已知ABCD是一个长方形,且M是ABCD所在平面上任意一点.求证：ABCDM证明：分别以AB、AD所在直线为x轴、y轴建立坐标系.设M（x,y）2222AMCMBMDMxy（b,0）（b,c）(0,c)（0,0）（x,y）222||AMxy222222||||=2222AMCMxybxcybc222||=()()CMxbyc222||=()BMxby222||=()DMxyc222222||||2222BMDMxybxcybc2222||||||||AMCMBMDMABCDMxy（b,0）（b,c）(0,c)（0,0）（x,y）ABCDM另证：以ABCD的中心O为原点，过点O分别与AB、AD平行的直线为x轴、y轴建立坐标系.设M（x，y）xy(a,c)(-a,c)（x,y）O(-a,-c)(a,-c)222||)()AMxayc（222||)()CMxayc（222222||||2222AMCMxyac222||)()BMxayc（222||)()DMxayc（222222||||2222BMDMxyacABCDMxy(-a,c)（x,y）O(-a,-c)(a,-c)(a,c)222||)AMxay（(a,c)ABCDMxy(a,0)(-a,c)(-a,0)(x,y)O222||)()CMxayc（222||)BMxay（222||)()DMxayc（三、坐标法在解决一些平面上的几何问题时，经常在平面上建立坐标系，以坐标系为桥梁，将几何问题转化为代数问题，通过代数运算研究几何图形的性质，这种方法称为坐标法．坐标法的基本步骤1.建立适当的坐标系，用坐标表示有关的量；2.进行有关的代数运算；3.将代数结果翻译成几何关系.例题3.已知如图，ABCD是圆内接四边形，AC⊥BD，E⊥AD，求证：ABCD'OE证明：分别以AC、BD所在直线为x轴、...