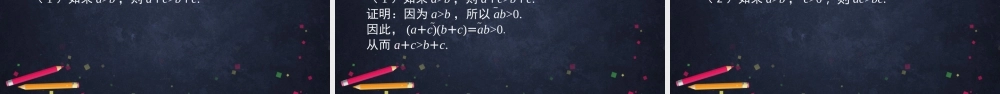0921高一【数学(人教B版)】不等式及其性质(1)-课件.pptxVIP免费

不等式及其性质（1）高一年级数学主讲人皇甫力超北京市第四中学北京市中小学空中课堂情境与问题右图是某居民小区的交通指示牌，下边标识是禁止鸣笛，上边标识提示机动车在小区内的时速v(单位：km/h)应满足：v5.v情境与问题用1kg的糖溶于4kg的水，可以得到浓度为20%的糖水.往此糖水中继续添加mkg的糖，容易知道糖水的浓度变大.用不等式可以表示为：其中m>0.v1+1,55mm不等关系与不等号我们用不等号“”“>”“<”“”“”连接两个实数或代数式，以表示它们之间的不等关系.含有不等号的式子，称为不等式.不等关系与不等号文字语言数学符号文字语言数学符号大于>至多小于<至少大于等于不少于小于等于不多于不等关系与不等号“”是指“>”或“=”.任给两个实数a，b，那么ab是指a>b或a=b.想一想请判断以下三个命题的真假：（1）53；（2）22；（3）22.想一想请判断以下三个命题的真假：（1）53；真（2）22；真（3）22.真两个实数比大小1.数量的多少与正整数的大小5个苹果比3个苹果多，经过抽象可得到正整数5和3的大小关系：5>3.两个实数比大小2.正整数的大小与实数的大小（1）实数与数轴上的点一一对应.两个实数比大小2.正整数的大小与实数的大小（2）数轴上的点往数轴正方向运动时，它所对应的实数会变大.例如，数轴上对应3的点向正方向移动2个单位，得到对应5的点.因此有5>3.两个实数比大小2.正整数的大小与实数的大小（3）两个实数比大小的代数法则设c>0，若ac=b，即ab=c，则有a>b；若a+c=b，即ab=c，则有a0，若ac=b，即ab=c，则有a>b；若a+c=b，即ab=c，则有a0a>b，ab<0a0a>b，ab=0a=b，ab<0a0，所以x2x>x2.等式的性质1.等式的性质（1）如果a=b，则a+c=b+c；（2）如果a=b，则ac=bc；（3）传递性：如果a=b，b=c，则a=c；（4）对称性：a=bb=a.不等式的性质2.不等式的性质（1）如果a>b，则a+c>b+c.（2）如果a>b，c>0，则ac>bc.（3）如果a>b，c<0，则acb，则a+c>b+c.不等式的性质...