0918高二【数学（人教B版）14】二面角（2)-课件.pptxVIP免费

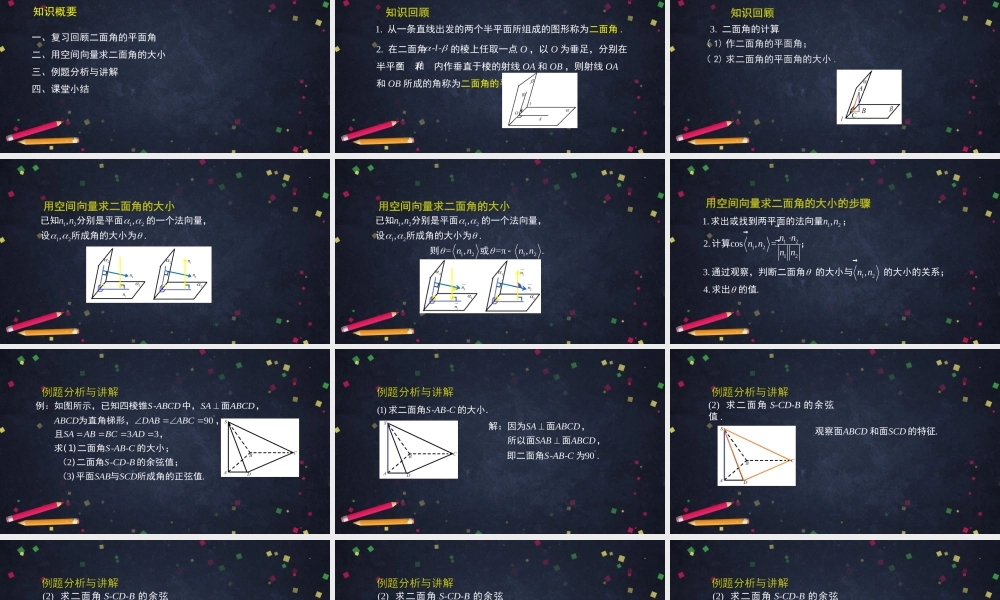
二面角（2)高二年级数学主讲人王秋寰北京市第四中学北京市中小学空中课堂知识概要一、复习回顾二面角的平面角二、用空间向量求二面角的大小三、例题分析与讲解四、课堂小结知识回顾2.在二面角的棱上任取一点O，以O为垂足，分别在半平面和内作垂直于棱的射线OA和OB，则射线OA和OB所成的角称为二面角的平面角.--l--l1.从一条直线出发的两个半平面所组成的图形称为二面角.知识回顾3.二面角的计算（1)作二面角的平面角；（2)求二面角的平面角的大小.用空间向量求二面角的大小121212,,,.nn�已知分别是平面的一个法向量，设所成角的大小为1n�2n�11n�2n�122用空间向量求二面角的大小121212,,,.nn�已知分别是平面的一个法向量，设所成角的大小为1212=,=π,.nnnn�则或用空间向量求二面角的大小的步骤12121212121.,2.cos,=3.,4..nnnnnnnnnn�����求出或找到两平面的法向量；计算；通过观察，判断二面角的大小与的大小的关系；求出的值例题分析与讲解-9033--2--3.SABCDSAABCDABCDDABABCSAABBCADSABCSCDBSABSCD例：如图所示，已知四棱锥中，面，为直角梯形，，且，求(1)二面角的大小；（)二面角的余弦值；（)平面与所成角的正弦值例题分析与讲解--90.SAABCDSABABCDSABC解：因为面，所以面面，即二面角为(1)--SABC求二面角的大小.例题分析与讲解(2)求二面角S-CD-B的余弦值..ABCDSCD观察面和面的特征例题分析与讲解.--.AAECDCDESESAABCDSEASCDB解：过作，交的延长线于，连接因为面，所以是二面角的平面角(2)求二面角S-CD-B的余弦值.tan.SASEAAE例题分析与讲解.3213.2cos13ACDDFBCFABCACDFCDCADCADC连接，过作于在中，，在中，在中，由余弦定理，(2)求二面角S-CD-B的余弦值.2cos13DEADEADEAD在中，，2.13DE所以2313例题分析与讲解(2)求二面角S-CD-B的余弦值.3tan131314cos14SAAESEAAESEA，所以，，14--.14SCDB即二面角的余弦值为例题分析与讲解(2)求二面角S-CD-B的余弦值.,,.,,,,.ADABASAADABASxyz�法二建系.两两互相垂直以为原点，的方向分别为轴轴轴的正方向，建立空间直角坐标系xyz(0,0,0)(1,0,0)(0,0,3)(0,3,0)(3,3,0).ADSBC，，，，例题分析与讲解(2)求二面角S-CD-B的余弦值.xyz(0,0,3).(1,0,3)(2,3,0).(,,)30,230.ASABCDDSDCSCDnxyznDSxznDCxy������...