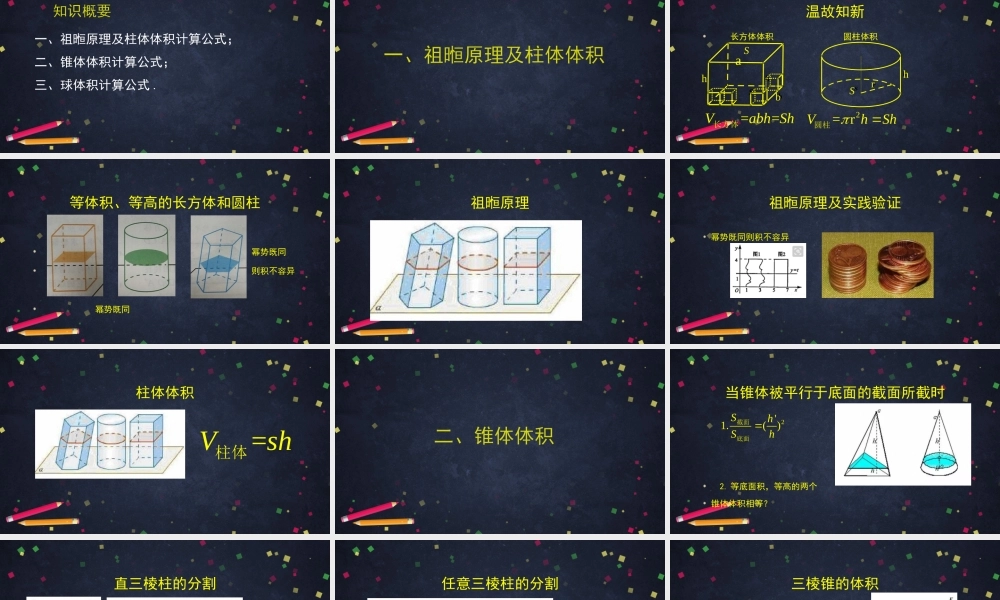
高一年级数学柱体、锥体、台体和球的体积主讲人徐晓阳北京市第四中学一、祖暅原理及柱体体积计算公式;二、锥体体积计算公式;三、球体积计算公式.知识概要一、祖暅原理及柱体体积长方体体积圆柱体积温故知新ahbS2=rVhSh圆柱==VabhSh长方体abhShrShSr等体积、等高的长方体和圆柱幂势既同则积不容异幂势既同祖暅原理祖暅原理及实践验证幂势既同则积不容异柱体体积=Vsh柱体二、锥体体积当锥体被平行于底面的截面所截时2.等底面积,等高的两个锥体体积相等?2'1.()ShSh截面底面直三棱柱的分割一个直三棱柱可分割为三个等体积的三棱锥任意三棱柱的分割任意一个三棱柱可分割为三个等体积的三棱锥三棱锥的体积任何一个三棱锥均可补形成一个与之等底面积、等高的三棱柱三棱锥的体积等于与其等底面积等高的三棱柱体积的1/3锥体的体积如果锥体的底面积为S,高为h,则锥体的体积计算公式为:1=3VSh锥体SSh*台体体积(可课下自学)所有台体都可看成一个锥体截取一个小锥体得到三、球体积祖暅原理可否用于球基于幂势既同的神奇构造hhhRRRhRORR幂势既同,积不容异R球的体积如果球的半径为R,那么球的体积计算公式为:34=3VR球OR猜猜右图的含义?感兴趣课下自查自学球体积另一经典思路(可课下自学)四、运用、巩固简单运用1例1.如图所示,在长方体中,求棱锥的体积与长方体的体积比ABCD-A'B'C'D'D'-A'CD解:设长方体的三条棱长分别为a,b,c,则长方体体积为,因为棱锥可以看成,所以所以,所求的体积比为1:6简单运用1ABCD-A'B'C'D'VabcD'-A'CDA'-D'CDD'-A'CDA'-D'CD1VV6abc简单运用2例2.如图,某铁质零件由一个正四棱柱和一个球组成,已知正四棱柱的底面边长与球的直径均为1cm,正四棱柱的高为2cm.现有这种零件一盒共50kg,取铁的密度为,π近似3.14.试计算这盒零件的个数.37.8/gcm简单运用2解:每个零件的体积为:因此每个零件的质量为:由此可估计零件的个数为50000254119.683341112()322()6cm(2)7.81.3(12)19.68()6g一、祖暅原理与柱体体积计算二、锥体体积计算及简单运用三、球体积计算及简单运用四、学习起始于课堂但绝不能就此终止(自学任务:台体体积公式?微积分思想)小结:课后任务1.通过整理课堂笔记,梳理体会教材在柱、锥、台、球体积推导过程中思路主线2.做课后配套练习P87,练习A,练习B*3.通过阅读课本P86《我国古代数学中球的体积公式》一文,结合自己的学习感悟,尝试做些与数学有关的拓展研究。