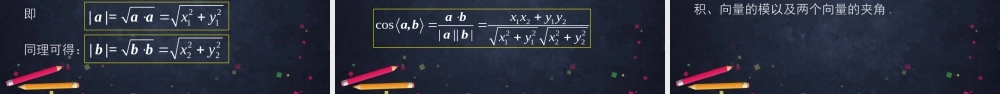0525高一数学（人教B版）--向量数量积的坐标运算--2PPT课件【公众号悦过学习分享】.pptxVIP免费

高一年级数学向量数量积的坐标运算主讲人李艳军北京师范大学良乡附属中学复习回顾：①向量数量积的定义及相关性质？||||cos，ababab2||,aaa即：||aaacos||||，ababab（是非零向量）a,b0abab复习回顾：②必修第二册学习过的平面向量坐标表示的定义？在平面直角坐标系中，分别给定与轴、轴正方向相同的单位向量之后，根据平面向量基本定理可知，对平面内的任意向量，有且只有一对实数，使得.axy12xyaeexy12，eexyae1e2123132O(,)xyax,y()a=12{}e,e这时我们称有序实数对是向量的坐标，记作.而且，是一组单位正交基底.根据向量数量积的定义，可得xyae1e2123132O(,)xyax,y()a=12{}e,e这时我们称有序实数对是向量的坐标，记作.而且，是一组单位正交基底.根据向量数量积的定义，可得112211cos01eeee122111cos900.eeeexyae1e2123132O向量可以用坐标表示，我们又学习了向量数量积的定义，那么向量的数量积可以用坐标表示吗？思考1：设你能用的坐标表示吗？1122,xyxy()()，，，a=b=，abab由平面向量坐标表示的定义可知，如果那么存在单位正交基底使得12{},,ee11,,xy()a=22xy(),,b=由平面向量坐标表示的定义可知，如果那么存在单位正交基底使得12{},,ee11,,xy()a=22xy(),,b=11122122++xyxy,a=eeb=ee于是11122122(+)(+)xyxyab=eeee于是11122122(+)(+)xyxyab=eeee1211121212211222+++xxxyyxyy=eeeeeeee于是11122122(+)(+)xyxyab=eeee1211121212211222+++xxxyyxyy=eeeeeeee1212+xxyy=从而1212+xxyyab=前面学习了向量数量积的性质，得出了向量模、以及两个向量夹角的余弦公式，这些公式可以用坐标表示吗？思考2：设且它们都不是零向量时，你能用的坐标表示出和1122xyxy()(),,,,a=b=,|a||b|cos,ab,ab吗？由向量数量积的性质及向量数量积的坐标表示得：由向量数量积的性质及向量数量积的坐标表示得：222111111()()=xyxyxy,,|a|=aa=即2211xy|a|=aa由向量数量积的性质及向量数量积的坐标表示得：222111111()()=xyxyxy,,|a|=aa=即2211xy|a|=aa同理可得：2222xy|b|=bb由向量数量积的性质及向量数量积的坐标表示得：121222221122cos||||xxyyxyxyaba,bab当,ab是非零向量时，小结：利用向量的坐标可以迅速的算出向量的数量积、向量的模以及两个向量的夹角.思考3：在平面直角坐标系中，如果你能利用向量的数量积得出这两点之间的距...