2.4.1平面向量的数量积及运算律(2)(1).pptVIP免费

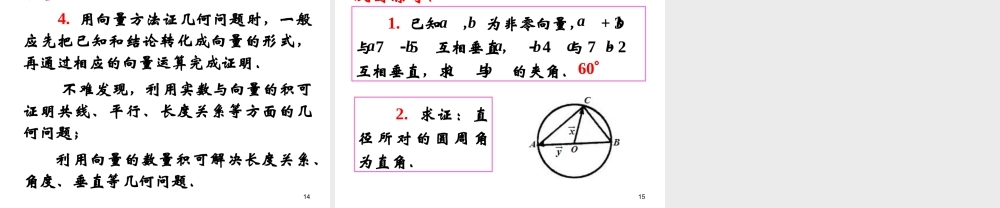
1平面向量的数量积及运算律（第二课时）2||||cos.abab1.平面向量的数量积:2.的几何意义:ab.cos的乘积的方向上的投影在长度与的等于数量积bababa33.平面向量的数量积的性质:,方向相同的单位向量，是与是非零向量，设beba的夹角，则与是ea(1)||cos.aea(2)0.abab22(3)||.aarr(4)cos.||||abab(5)||||||.ababB1bBaAOe4练习�在三角形ＡＢＣ中，ＡＢ＝ａ，ＢＣ＝ｂ，且ａｂ＞０，则三角形ＡＢＣ是（）三角形5向量的数量积的运算律：，则向量的和实数、、已知向量cba：数量积满足下列运算律(1)abbarrrr(2)()()().abababrrrrrr(3)().abcacbcrrrrrrrbaba)(可以简写成(交换律)(分配律)6的证明：运算律)3(,O如图，任取一点,bAB,cOC,aOA作OBba则aAcBCb1AB1Oθθ1θ2上的投影在OCOBABOA上的在与在恰是OCbOCa即投影之和,12||cos||cos||cos,ababrrrr||||coscabrrr().abcacbcrrrrrrr12||||cos||||cos,cacbrrrr7在实数中，有(ab)c=a(bc)，向量中是否也有?为什么?答：未必成立()()abcabc因为左端是与共线的向量，而右端是与共线的向量，但一般与不共线．acca所以，向量的内积不满足结合律．8222(1)()2;abaabb22(2)()).ababab（2(1)())()ababab（)()abaabb（22abaabb(2)())()()abababaabb（例1求证：证明：22abaabb22.ab222.aabb9(3)与所成角的余弦值．例2已知||=6，||=4，与的夹角...