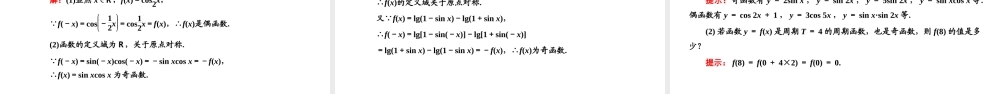5.4.2正弦函数、余弦函数的性质明确目标发展素养1.理解周期函数、周期、最小正周期的定义.2.会求正弦函数、余弦函数的周期,并会应用.3.掌握正弦函数、余弦函数的奇偶性,会判断简单三角函数的奇偶性.1.通过理解函数的周期性,培养逻辑推理和数学抽象素养.2.通过奇偶性的应用,提升数学运算素养.(一)教材梳理填空1.函数的周期性:(1)周期函数:一般地,设函数f(x)的定义域为D,如果存在一个,使得对每一个x∈D都有x+T∈D,且,那么函数f(x)就叫做周期函数.叫做这个函数的周期.(2)最小正周期:如果在周期函数f(x)的所有周期中存在一个最小的,那么这个最小就叫做f(x)的.非零常数Tf(x+T)=f(x)非零常数T正数正数最小正周期第一课时正弦函数、余弦函数的周期性与奇偶性2.正弦函数、余弦函数的周期性和奇偶性:[微思考](1)所有的函数都具有周期性吗?提示:并不是每一个函数都是周期函数.(2)周期函数的周期是唯一的吗?提示:若函数具有周期性,则其周期也不一定唯一.函数y=sinxy=cosx周期2kπ(k∈Z且k≠0)2kπ(k∈Z且k≠0)最小正周期__________奇偶性______________2π2π奇函数偶函数(二)基本知能小试1.判断正误(1)若sin2π3+π6=sinπ6,则2π3是函数y=sinx的一个周期.()(2)所有的周期函数都有最小正周期.()(3)函数y=sinx是奇函数.()答案:(1)×(2)×(3)×2.函数y=2cos2x+π2是()A.周期为π的奇函数B.周期为π的偶函数C.周期为2π的奇函数D.周期为2π的偶函数解析:y=2cos2x+π2=-2sin2x,它是周期为π的奇函数.答案:A3.函数y=3sinx+5的最小正周期是________.解析:设f(x)=3sinx+5,x∈R.因为f(x+2π)=3sin(x+2π)+5=3sinx+5=f(x),所以y=3sinx+5的最小正周期是2π.答案:2π4.若函数f(x)是周期为3的周期函数,且f(-1)=2021,则f(2)=________.解析:因为函数f(x)是周期为3的周期函数,所以f(2)=f(2-3)=f(-1)=2021.答案:2021题型一三角函数的周期【学透用活】1.对函数最小正周期的两点说明(1)最小正周期是指能使函数值重复出现的自变量x要加上的那个最小正数,这个正数是对x而言的,如y=sin2x的最小正周期是π,因为y=sin2x=sin(2x+2π)=sin[2(x+π)],即π是使函数值重复出现的自变量x加上的最小正数,π是对x而言的,而非2x.(2)并不是所有的周期函数都有最小正周期,比如,常数函数f(x)=c,任意一个正实数都是它的周期,因而不存在最小...