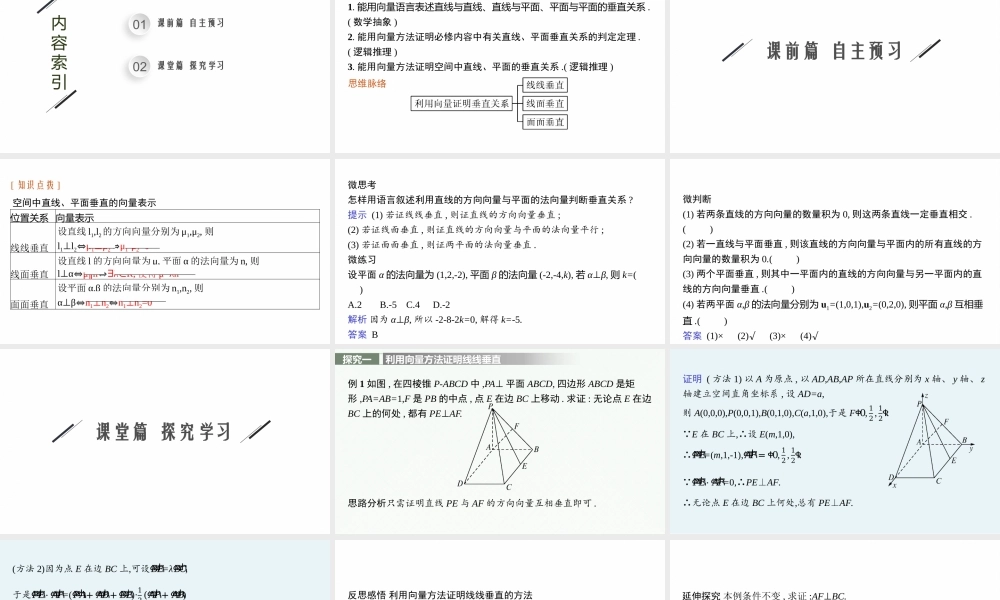
高中同步学案优化设计GAOZHONGTONGBUXUEANYOUHAUSHEJI第2课时空间中直线、平面的垂直第一章2021内容索引0102课前篇自主预习课堂篇探究学习课标阐释思维脉络1.能用向量语言表述直线与直线、直线与平面、平面与平面的垂直关系.(数学抽象)2.能用向量方法证明必修内容中有关直线、平面垂直关系的判定定理.(逻辑推理)3.能用向量方法证明空间中直线、平面的垂直关系.(逻辑推理)课前篇自主预习[知识点拨]空间中直线、平面垂直的向量表示位置关系向量表示线线垂直设直线l1,l2的方向向量分别为μ1,μ2,则l1⊥l2⇔μ1⊥μ2⇔μ1·μ2=0线面垂直设直线l的方向向量为μ,平面α的法向量为n,则l⊥α⇔μ∥n⇔∃λ∈R,使得μ=λn面面垂直设平面α,β的法向量分别为n1,n2,则α⊥β⇔n1⊥n2⇔n1⊥n2=0微思考怎样用语言叙述利用直线的方向向量与平面的法向量判断垂直关系?提示(1)若证线线垂直,则证直线的方向向量垂直;(2)若证线面垂直,则证直线的方向向量与平面的法向量平行;(3)若证面面垂直,则证两平面的法向量垂直.微练习设平面α的法向量为(1,2,-2),平面β的法向量(-2,-4,k),若α⊥β,则k=()A.2B.-5C.4D.-2解析因为α⊥β,所以-2-8-2k=0,解得k=-5.答案B微判断(1)若两条直线的方向向量的数量积为0,则这两条直线一定垂直相交.()(2)若一直线与平面垂直,则该直线的方向向量与平面内的所有直线的方向向量的数量积为0.()(3)两个平面垂直,则其中一平面内的直线的方向向量与另一平面内的直线的方向向量垂直.()(4)若两平面α,β的法向量分别为u1=(1,0,1),u2=(0,2,0),则平面α,β互相垂直.()答案(1)×(2)√(3)×(4)√课堂篇探究学习探究一利用向量方法证明线线垂直例1如图,在四棱锥P-ABCD中,PA⊥平面ABCD,四边形ABCD是矩形,PA=AB=1,F是PB的中点,点E在边BC上移动.求证:无论点E在边BC上的何处,都有PE⊥AF.思路分析只需证明直线PE与AF的方向向量互相垂直即可.证明(方法1)以A为原点,以AD,AB,AP所在直线分别为x轴、y轴、z轴建立空间直角坐标系,设AD=a,则A(0,0,0),P(0,0,1),B(0,1,0),C(a,1,0),于是Fቀ0,12,12ቁ. E在BC上,∴设E(m,1,0),∴𝑃𝐸ሬሬሬሬሬԦ=(m,1,-1),𝐴𝐹ሬሬሬሬሬԦ=ቀ0,12,12ቁ. 𝑃𝐸ሬሬሬሬሬԦ·𝐴𝐹ሬሬሬሬሬԦ=0,∴PE⊥AF.∴无论点E在边BC上何处,总有PE⊥AF.(方法2)因为点E在边BC上,可设𝐵𝐸ሬሬሬሬሬԦ=λ𝐵𝐶ሬሬሬሬሬԦ,于是𝑃𝐸ሬሬሬሬሬԦ·𝐴𝐹ሬሬሬሬሬԦ=(𝑃𝐴ሬሬሬሬሬԦ+𝐴𝐵ሬሬሬሬሬԦ+𝐵𝐸ሬሬሬሬሬԦ)·12(𝐴𝑃ሬሬሬሬሬԦ+𝐴𝐵ሬ...