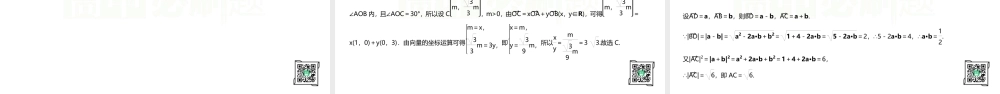数学必修第二册RJA00专题1平面向量的综合应用解析专题1平面向量的综合应用刷难关B题型1平面向量基本定理的应用1.设a是已知的平面向量,且a≠0.关于向量a的分解,有如下四个命题:①给定向量b,总存在向量c,使a=b+c;②给定向量b和c,总存在实数λ和μ,使a=λb+μc;③给定单位向量b和正数μ,总存在单位向量c和实数λ,使a=λb+μc;④给定正数λ和μ,总存在单位向量b和单位向量c,使a=λb+μc.上述命题中的向量b,c和a在同一平面内且两两不共线,则真命题的个数是()A.1B.2C.3D.4给定向量a和b,只需求得其差向量a-b即为所求的向量c,故总存在向量c,使a=b+c,故①是真命题;由于向量b,c和a在同一平面内且两两不共线,故{b,c}可作基底,由平面向量基本定理可知②是真命题;由题意,当μ<|a|sin〈a,b〉时,不存在符合题意的单位向量c和实数λ,故③是假命题;因为λ和μ为正数,所以λb和μc代表与原向量同向且有固定长度的向量,这就使得向量a不一定能用两个单位向量的组合表示出来,故不一定能使a=λb+μc成立,故④是假命题.故选B.解析专题1平面向量的综合应用刷难关B2.[黑龙江鸡西一中2020高一期中]△ABC是边长为4的等边三角形,AD→=13DC→,则BD→·BC→=()A.-2B.10C.12D.14因为△ABC是边长为4的等边三角形,AD→=13DC→,所以CD→=34CA→=34(BA→-BC→),所以BD→·BC→=(BC→+CD→)·BC→=BC→2+34(BA→-BC→)·BC→=16+34BA→·BC→-34BC→2=16+34×4×4×cos60°-34×16=10.故选B.解析专题1平面向量的综合应用刷难关A3.在△ABC中,BD→=DC→,AP→=2PD→,BP→=λAB→+μAC→,则λ+μ=()A.-13B.13C.-12D.12因为BD→=DC→,AP→=2PD→,所以P为△ABC的重心,所以AD→=12AB→+12AC→=32AP→,即AP→=13AB→+13AC→,所以BP→=AP→-AB→=-23AB→+13AC→.因为BP→=λAB→+μAC→,所以λ=-23,μ=13,λ+μ=-13.故选A.专题1平面向量的综合应用刷难关44.如图,已知△ABC的面积为14cm2,D,E分别为边AB,BC上的点,且AD︰DB=BE︰EC=2︰1,AE,CD交于点P,则△APC的面积为________cm2.解析专题1平面向量的综合应用刷难关设AB→=a,BC→=b,以{a,b}为一个基底,则AE→=a+23b,DC→=13a+b. 点A,P,E与点D,P,C分别共线,∴存在实数λ和μ,使AP→=λAE→=λa+23λb,DP→=μDC→=13μa+μb.又 AP→=AD→+DP→=23+13μa+μb,∴λ=23+...