习题课 三角函数的图象与性质.pptxVIP免费

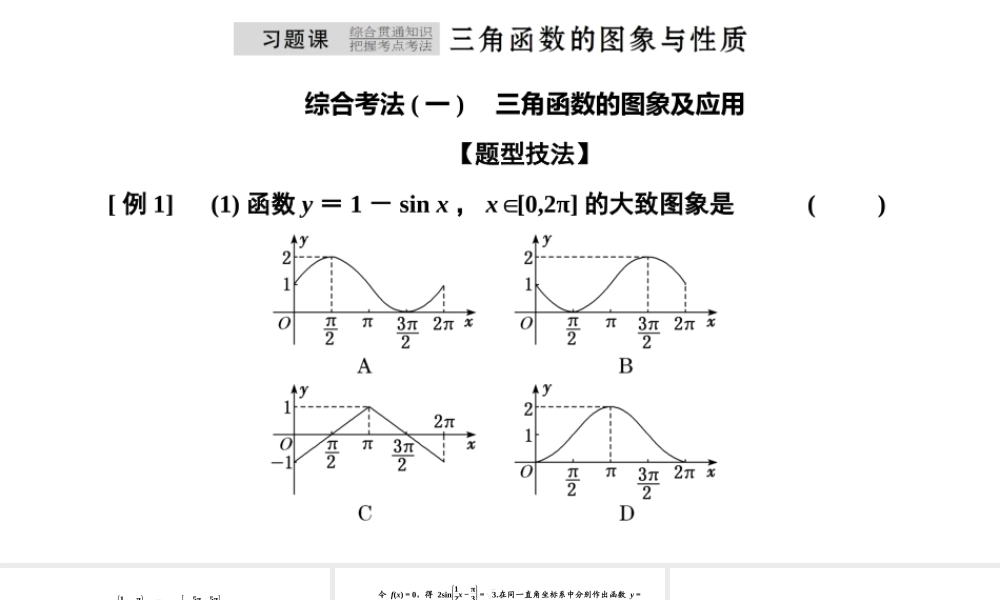
综合考法(一)三角函数的图象及应用【题型技法】[例1](1)函数y＝1－sinx，x[0,2π]∈的大致图象是()(2)已知函数f(x)＝2sin12x－π3－3，x∈－5π2，5π2，则函数f(x)的零点个数为()A．2B．3C．4D．5[解析](1)当x＝π2时，y＝0；当x＝0时，y＝1；当x＝2π时，y＝1.结合正弦函数的图象可知B正确．(2) f(x)＝2sin12x－π3－3，x∈－5π2，5π2，令f(x)＝0，得2sin12x－π3＝3.在同一直角坐标系中分别作出函数y＝2sin12x－π3，y＝3的图象如图所示，观察图象可知，它们在－5π2，5π2上有3个交点，即函数f(x)的零点个数为3.[答案](1)B(2)B[方法技巧]解三角函数图象有关问题的注意点(1)熟记正弦、余弦、正切函数的图象形状及特点，尤其熟记正切函数的图象的画法、渐近线等．(2)要善于利用函数y＝f(x)的图象来作y＝|f(x)|及y＝f(|x|)的图象．(3)在研究方程的实根个数时，如果不能解出方程，一般转化为研究两个函数的图象的交点个数问题．【集训冲关】1．设函数f(x)＝sinx＋π3(x∈R)，则f(x)()A．在区间2π3，7π6上是增函数B．在区间－π，－π2上是减函数C．在区间－π3，π4上是增函数D．在区间π3，5π6上是减函数解析：函数f(x)＝sinx＋π3(x∈R)的图象如图所示，由图可知函数f(x)＝sinx＋π3(x∈R)在区间2π3，7π6上是增函数．故选A.答案：A2．函数f(x)＝xcosx(－π≤x≤π)的图象可能是()解析：易知函数f(x)的定义域关于原点对称，且f(－x)＝－xcos(－x)＝－xcosx＝－f(x)，则函数f(x)是奇函数，图象关于原点对称，排除B、D；f(π)＝πcosπ＝－π＜0，排除C，故选A.答案：A3．函数f(x)＝cos2x(x∈[－π，2π])的图象与函数g(x)＝sinx的图象的交点的横坐标的和为()A．2πB.5π3C.7π6D．π解析：根据题意，作出函数f(x)和g(x)的图象如图所示．由图可知，两个函数在[－π，2π]内有四个交点，由对称性，可知x1＋x42＝π2，x2＋x32＝π2.∴x1＋x2＋x3＋x4＝2π.答案：A综合考法(二)三角函数的性质及应用【题型技法】[例2](1)(多选)关于函数f(x)＝|tanx|的性质，下列叙述正确的是()A．f(x)的最小正周期为π2B．f(x)是偶函数C．f(x)的图象关于直线x＝kπ2(k∈Z)对称D．f(x)在每一个区间kπ，kπ＋π2(k∈Z...