习题课成对数据的统计分析.pptVIP免费

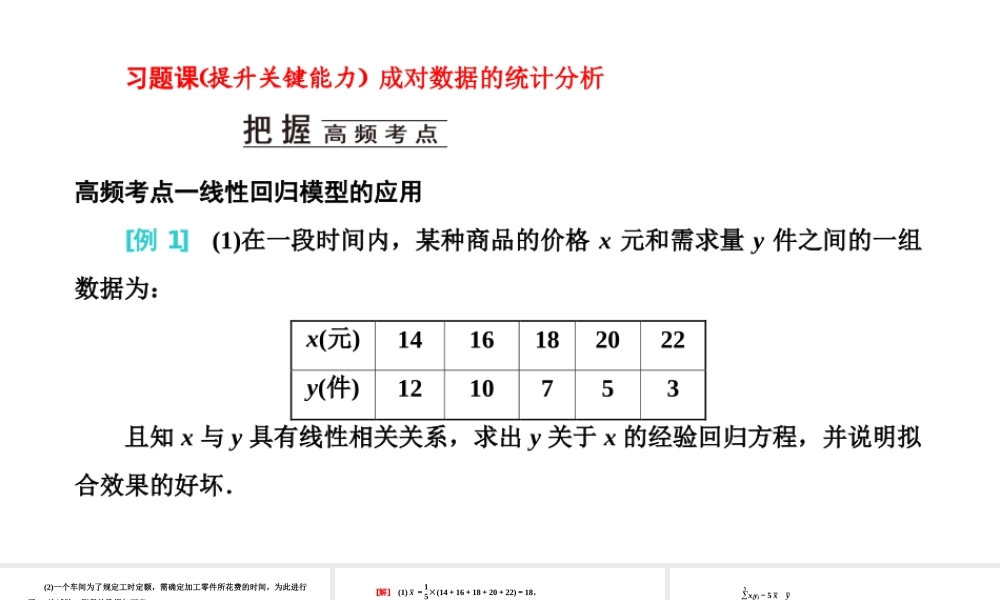
习题课提升关键能力成对数据的统计分析高频考点一线性回归模型的应用[例1](1)在一段时间内，某种商品的价格x元和需求量y件之间的一组数据为：x(元)1416182022y(件)1210753且知x与y具有线性相关关系，求出y关于x的经验回归方程，并说明拟合效果的好坏．(2)一个车间为了规定工时定额，需确定加工零件所花费的时间，为此进行了10次试验，测得的数据如下表：零件数x/个102030405060708090100加工时间y/min627275818595103108112127①作出散点图，并初步判断是否线性相关；②若线性相关，求经验回归方程；③求出相关指数；④作出残差图；⑤进行残差分析．[解](1)x－＝15×(14＋16＋18＋20＋22)＝18，y－＝15×(12＋10＋7＋5＋3)＝7.4，i＝15x2i＝142＋162＋182＋202＋222＝1660，i＝15y2i＝122＋102＋72＋52＋32＝327，i＝15xiyi＝14×12＋16×10＋18×7＋20×5＋22×3＝620，所以b^＝i＝15xiyi－5x－y－i＝15x2i－5x－2＝620－5×18×7.41660－5×182＝－1.15，a^＝7.4＋1.15×18＝28.1，所以y对x的经验回归方程为y^＝－1.15x＋28.1，列出残差表为yi－y^i00.3－0.4－0.10.2yi－y－4.62.6－0.4－2.4－4.4所以i＝15(yi－y^i)2＝0.3，i＝15(yi－y－)2＝53.2，R2＝1－i＝15yi－y^i2i＝15yi－y－2≈0.994.因为R2≈0.994接近于1，所以拟合效果很好．(2)①作出散点图，如图所示．由图可知，x，y线性相关．②x与y的关系可以用线性经验回归模型来拟合，不妨设经验回归模型为y^＝b^x＋a^.将数据代入相应公式可得数据表：序号零件个数xi(个)加工时间yi(min)xiyix2i110626201002207214404003307522509004408132401600550854250250066095570036007701037210490088010886406400990112100808100101001271270010000∑5509205613038500∴x＝55，y＝92，∴b^＝i＝110xiyi－10x－y－i＝110x2i－10x－2＝56130－10×55×9238500－10×552＝553825≈0.670，a^＝y－－b^x－＝92－553825×55＝82715≈55.133，∴经验回归方程为y^＝0.670x＋55.133.③利用所求经验回归方程求出下列数据.y^i61.83368.53375.23381.93388.633yi－y^i0.1673.467－0.233－0.933－3.633yi－y－－30－20－17－11－7y^i95.333102.033108.733115.433122.133yi－y^i－0.3330.967－0.733－3.4334.867yi－y－311162035∴R2＝1－i＝110yi－y^i2i＝110yi－y2≈0.983.④ ei＝yi－y^i，利用上表中数据作出残差图，如图所示．⑤由散点图可以看出x与y有很强的线性...