0615高二数学（选修-人教B版）-离散型随机变量及其分布列（3）-2PPT.pptxVIP免费

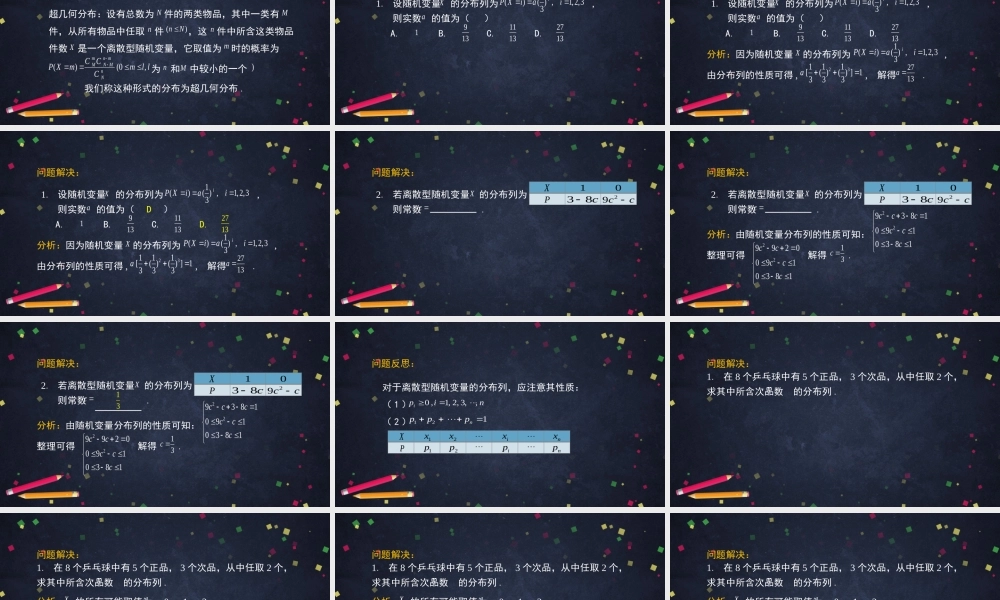
离散型随机变量及其分布列（3）高二年级数学主讲人：郭方奇北京师范大学第二附属中学概念回顾：随机变量：如果随机试验可能出现的结果可以用一个变量来表达，并且是随着试验的结果的不同而变化的，我们把这样的变量叫做一个随机变量.XXX概念回顾：例如：投掷一枚骰子，观察向上的点数，这个随机试验的所有结果，我们可以用一个变量来表达，的所有可能取值是1，2，3，4，5，6，是一个随机变量.XXX概念回顾：离散型随机变量：如果随机变量的所有可能取值都能一一列举出来，则称为离散型随机变量.XX概念回顾：例如：投掷骰子的随机试验，其结果的取值是可以一一列举出来的，则称为离散型随机变量.XX概念回顾：反例：从中随机取一个实数，这个随机试验的结果是不能一一列举出来的，则不能称其为离散型随机变量.[0,1]概念回顾：离散型随机变量的分布列：（1）如果的所有可能取值为（2）取每一个值的概率为X12,,,nxxxXix12,,,npppXP1x2xixnx1p2pipnp我们称这个表为离散型随机变量的分布列.X概念回顾：离散型随机变量的分布列的性质：（1）（2）0,1,2,3,,ipin121npppXP1x2xixnx1p2pipnp概念回顾：二点分布：如果离散型随机变量的分布列为其中则称离散型随机变量服从参数为X01,1,pqppXP10pq的二点分布.X概念回顾：二点分布：如果离散型随机变量的分布列为其中则称离散型随机变量服从参数为X01,1,pqppXP10pq的二点分布.例如：抛掷一枚硬币.X概念回顾：超几何分布：设有总数为件的两类物品，其中一类有件，从所有物品中任取件，这件中所含这类物品件数是一个离散型随机变量，它取值为时的概率为NX()(0,)mnmMNMnNCCPXmmllC为和中较小的一个Mn()nNnmnM我们称这种形式的分布为超几何分布.1.设随机变量的分布列为,则实数的值为（）A.B.C.D.问题解决：X1()(),1,2,33iPXiaia1913271311131.设随机变量的分布列为,则实数的值为（）A.B.C.D.问题解决：X1()(),1,2,33iPXiaia191327131113分析：因为随机变量的分布列为,由分布列的性质可得,,解得.X1()(),1,2,33iPXiai23111[()()]1333a2713a1.设随机变量的分布列为,则实数的值为（D）A.B.C.D.问题解决：X1()(),1,2,33iPXiaia191327131113分析：因为随机变量的分布列为,由分布列的性质可得,,解得.X1()(),1,2,33iPXiai23111[()()]1333a2713a2.若离散型...