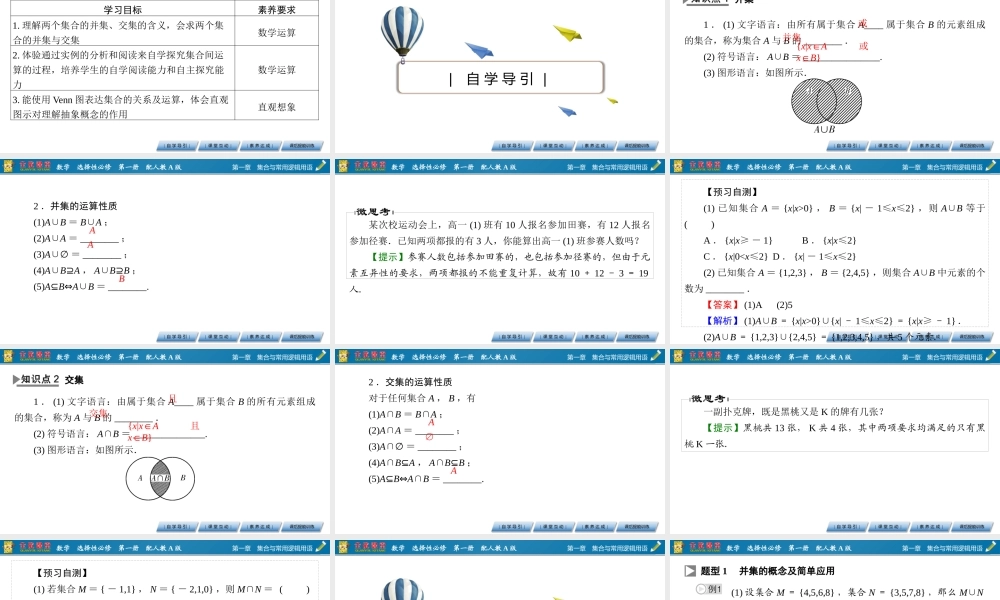
第一章集合与常用逻辑用语1.3集合的基本运算第1课时并集与交集第一章集合与常用逻辑用语数学选择性必修第一册配人教A版|自学导引||课堂互动||素养达成|课后提能训练学习目标素养要求1.理解两个集合的并集、交集的含义,会求两个集合的并集与交集数学运算2.体验通过实例的分析和阅读来自学探究集合间运算的过程,培养学生的自学阅读能力和自主探究能力数学运算3.能使用Venn图表达集合的关系及运算,体会直观图示对理解抽象概念的作用直观想象第一章集合与常用逻辑用语数学选择性必修第一册配人教A版|自学导引||课堂互动||素养达成|课后提能训练|自学导引|第一章集合与常用逻辑用语数学选择性必修第一册配人教A版|自学导引||课堂互动||素养达成|课后提能训练1.(1)文字语言:由所有属于集合A____属于集合B的元素组成的集合,称为集合A与B的________.(2)符号语言:A∪B=________________.(3)图形语言:如图所示.或并集并集{x|x∈A或x∈B}第一章集合与常用逻辑用语数学选择性必修第一册配人教A版|自学导引||课堂互动||素养达成|课后提能训练2.并集的运算性质(1)A∪B=B∪A;(2)A∪A=________;(3)A∪∅=________;(4)A∪B⊇A,A∪B⊇B;(5)A⊆B⇔A∪B=________.AAB第一章集合与常用逻辑用语数学选择性必修第一册配人教A版|自学导引||课堂互动||素养达成|课后提能训练某次校运动会上,高一(1)班有10人报名参加田赛,有12人报名参加径赛.已知两项都报的有3人,你能算出高一(1)班参赛人数吗?【提示】参赛人数包括参加田赛的,也包括参加径赛的,但由于元素互异性的要求,两项都报的不能重复计算,故有10+12-3=19人.第一章集合与常用逻辑用语数学选择性必修第一册配人教A版|自学导引||课堂互动||素养达成|课后提能训练【预习自测】(1)已知集合A={x|x>0},B={x|-1≤x≤2},则A∪B等于()A.{x|x≥-1}B.{x|x≤2}C.{x|00}∪{x|-1≤x≤2}={x|x≥-1}.(2)A∪B={1,2,3}∪{2,4,5}={1,2,3,4,5},共5个元素.第一章集合与常用逻辑用语数学选择性必修第一册配人教A版|自学导引||课堂互动||素养达成|课后提能训练1.(1)文字语言:由属于集合A____属于集合B的所有元素组成的集合,称为A与B的________.(2)符号语言:A∩B=_______________.(3)图形语言:如图所示.且交集交集{x|x∈A且x∈B}第一章集合与常...