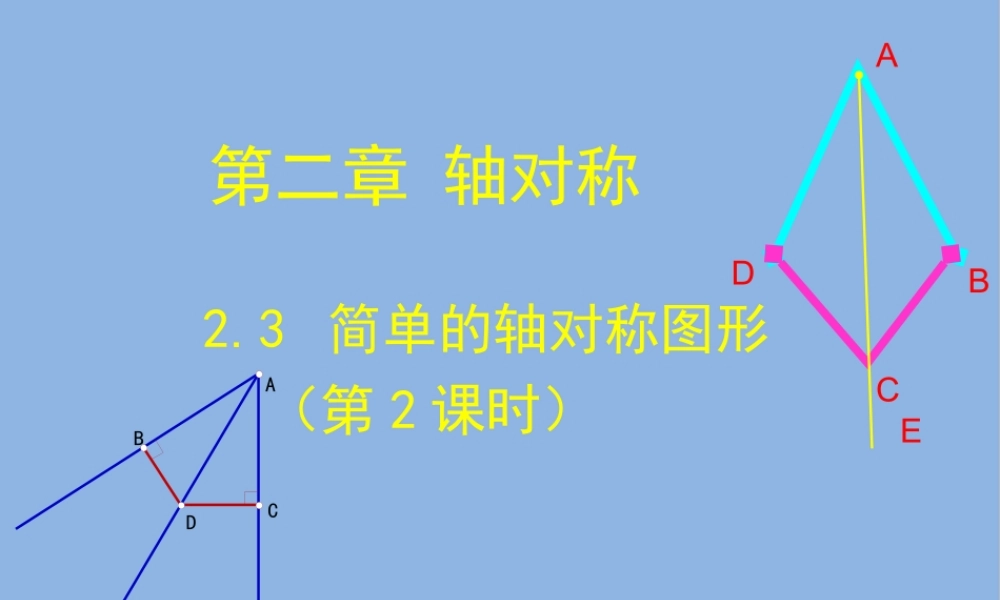
第二章轴对称2.3简单的轴对称图形(第2课时)ADBCEADCB不利用工具,请你将一张用纸片做的角分成两个相等的角,你有什么办法?AOBC再打开纸片,看再打开纸片,看看折痕与这个角有何关系?看折痕与这个角有何关系?(对折)C结论:角是轴对称图形,对称轴是角平分线所在的直线.ABO有一个简易平分角的仪器(如图),其中AB=AD,BC=DC,将A点放角的顶点,AB和AD沿AC画一条射线AE,AE就是∠BAD的平分线,为什么?对这种可以折叠的角可以用折叠方法的角平分线,对不能折叠的角怎样得到其角平分线?证明:在△ACD和△ACB中AD=AB(已知)DC=BC(已知)CA=CA(公共边)∴△ACDACB≌△(SSS)∴∠CAD=CAB∠(全等三角形的对应边相等)∴AC平分∠DAB(角平分线的定义)ADBCE根据角平分仪的制作原理怎样用尺规作一个角的平分线?(不用角平分仪或量角器)OABCENOMCENM2.分别以M,N为圆心.大于MN的长为半径作弧.两弧在∠AOB的内部交于C.21用尺规作角的平分线的方法用尺规作角的平分线的方法AABBOOMMNNCC作法:1.以O为圆心,适当长为半径作弧,交OA于M,交OB于N.3.作射线OC.则射线OC即为所求.将∠AOB对折,再折出一个直角三角形(使第一条折痕为斜边),然后展开,观察两次折叠形成的三条折痕,你能得出什么结论?(2)猜想:可以看一看,第一条折痕是∠AOB的平分线OC,第二次折叠形成的两条折痕PD,PE是角的平分线上一点到∠AOB两边的距离,这两个距离相等.角的平分线上的点到这个角的两边的距离相等.探究角平分线的性质已知:如图,OC是∠AOB的平分线,点P在OC上,PDOA⊥,PEOB⊥,垂足分别是D,E.求证:PD=PE证明: PDOA⊥,PEOB⊥(已知)∴∠PDO=PEO=90∠(垂直的定义)在△PDO和△PEO中∴PD=PE(全等三角形的对应边相等)∠PDO=PEO∠AOC=BOC∠∠OP=OP∴△PDOPEO≌△(AAS)DPEAOBC(3)验证猜想角的平分线上的点到角的两边的距离相等.角平分线上角平分线上的点到角两的点到角两边的距离相边的距离相等等..(4)得到角平分线的性质:利用此性质怎样书写推理过程?角平分线的性质定理:角的平分线上的点到角的两边的距离相等用符号语言表示为:AOBPED12 ∠1=∠2PD⊥OA,PE⊥OB∴PD=PE(角的平分线上的点到角的两边的距离相等)推理的理由有三个,必须写完全,不能少了任何一个.角平分线的性质角的平分线上的点到角的两边的距离相等。角的平分线上的点到角的两边的距离相等。BADOPEC定理应用所具备的条件:(1)角的平分线;(2)点在...