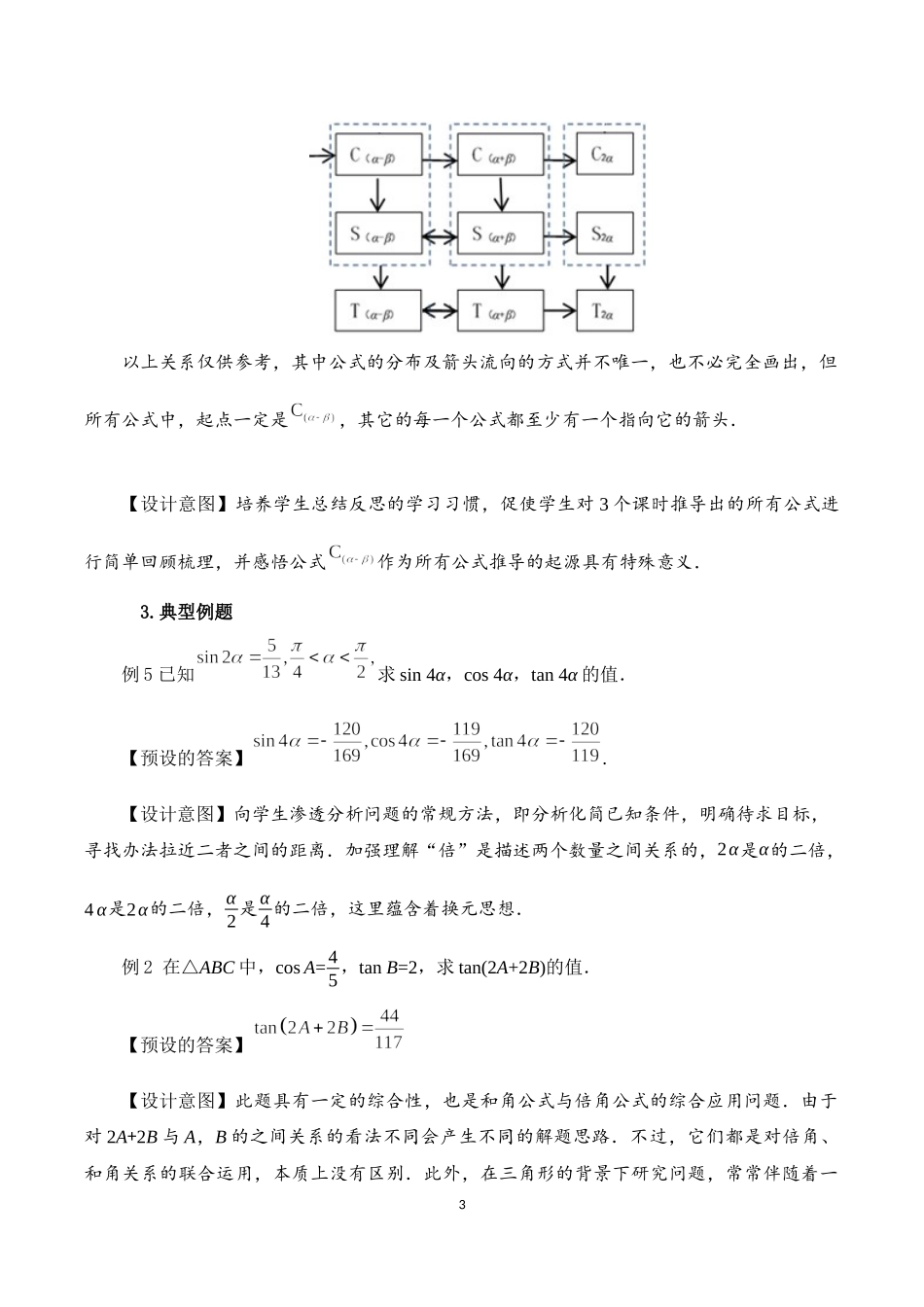
15.5.1两角和与差的正弦、余弦、正切公式(第3课时)(人教A版普通高中教科书数学必修第一册第五章)深圳高级中学(集团)东校区张培兰一、教学目标1.经历从和角公式推导二倍角公式的过程,体会公式各个公式间的内在联系,认识整个公式体系的生成过程,发展学生逻辑推理素养.2.掌握并运用二倍角公式,及其变形形式,,能正确运用二倍角公式进行证明化简、求值;通过综合运用公式,掌握思想方法,来发展学生逻辑推理能力、分析问题,解决问题能力、数学运算素养.二、教学重难点1.二倍角公式的推导及灵活运用.2.二倍角的相对性.三、教学过程1.复习回顾活动:让学生默写两角和与差的正弦、余弦、正切公式,并请同学回想并回答公式的推导过程以及描述几个公式之间的联系。【活动预设】学生大体能正确默写六个公式,对于公式的推理及六个公式之间的联系可能需要老师引导回顾。2.新知探究问题1:你能利用推导出的公式吗?你能用不同的方法推出这些公式吗?【活动预设】学生独立进行推导,教师巡视并收集学生的不同证法,或请学生将不同的证法列举在黑板上.【预设的答案】这里不同的证法主要体现在两个方面:一是推导的依据具有多样性,例如可以将中替换为推得,也可以由中的替换为,而推导公式时,可以从出发,也可以由合作推出;二是推导的顺序具有多样性,学生可以自行2设计三个二倍角公式的证明顺序,由于推导其中最后一个公式时可以借助已推出的两个公式,因此不同的顺序可能会导致最后一步有所差异..三个公式分别简记为,,.【设计意图】给学生一定的自由度,由学生自己制定计划,并完成二倍角公式的证明.问题2:如果要求二倍角的余弦公式()中仅含的正弦或仅含余弦,那么你能得到怎样的结论?【活动预设】学生独立进行推导.【预设的答案】,.【设计意图】引导学生发现公式的两种变形形式,为下一课时半角公式做好铺垫.教师讲授:以上五个公式都叫做二倍角公式,或倍角公式.倍角公式给出了任意角的三角函数与的三角函数之间的关系.这里的“倍角”专指“二倍角”,遇到“三倍角”等名词时,“三”字等不可省去.此外,这里的“倍角”是一种相对的概念.不仅“”是“”的二倍角,而且“”是“”的二倍角,“”是“”的二倍角,“”是“”的二倍角.问题3:从和角公式、差角公式、倍角公式的推导过程可以发现,这些公式之间存在紧密的逻辑联系,你能设计一张结构图描述它们之间的推出关系吗?【活动预设】学生进行归纳整理,作出结构图,然后小...