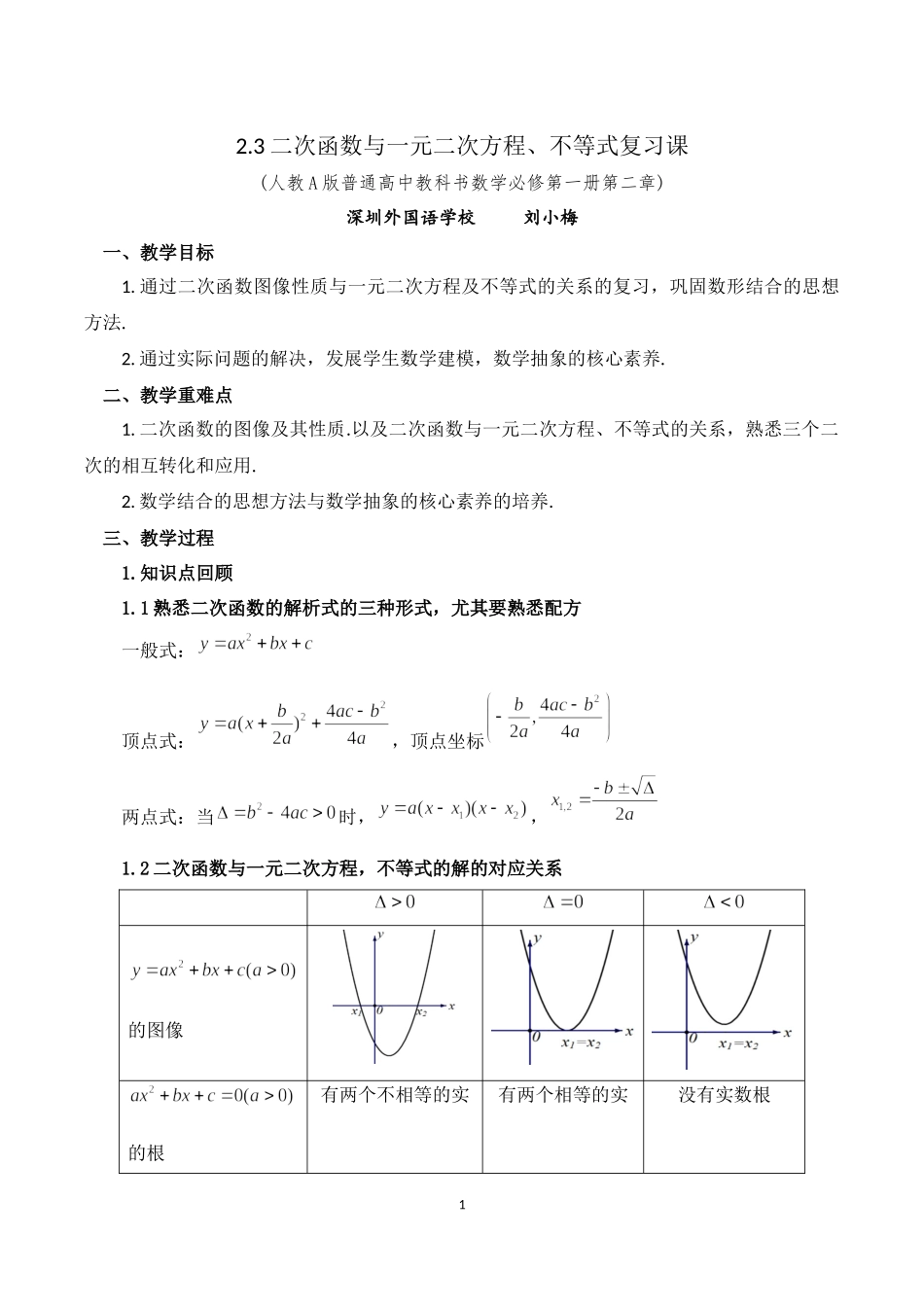
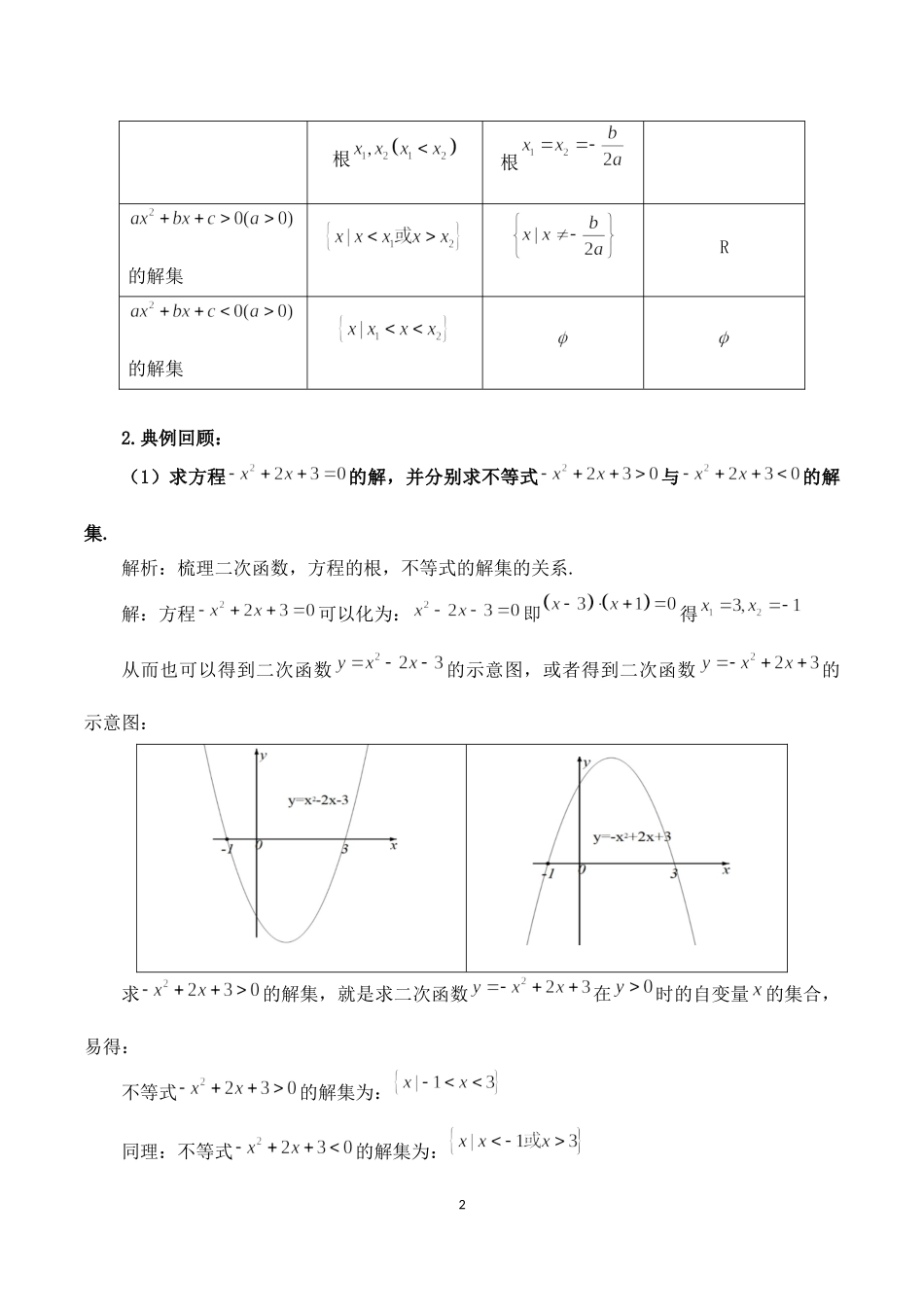
12.3二次函数与一元二次方程、不等式复习课(人教A版普通高中教科书数学必修第一册第二章)深圳外国语学校刘小梅一、教学目标1.通过二次函数图像性质与一元二次方程及不等式的关系的复习,巩固数形结合的思想方法.2.通过实际问题的解决,发展学生数学建模,数学抽象的核心素养.二、教学重难点1.二次函数的图像及其性质.以及二次函数与一元二次方程、不等式的关系,熟悉三个二次的相互转化和应用.2.数学结合的思想方法与数学抽象的核心素养的培养.三、教学过程1.知识点回顾1.1熟悉二次函数的解析式的三种形式,尤其要熟悉配方一般式:顶点式:,顶点坐标两点式:当时,,1.2二次函数与一元二次方程,不等式的解的对应关系的图像的根有两个不相等的实有两个相等的实没有实数根2根根的解集R的解集2.典例回顾:(1)求方程的解,并分别求不等式与的解集.解析:梳理二次函数,方程的根,不等式的解集的关系.解:方程可以化为:即得从而也可以得到二次函数的示意图,或者得到二次函数的示意图:求的解集,就是求二次函数在时的自变量的集合,易得:不等式的解集为:同理:不等式的解集为:3方法总结:二次函数的图像与x轴的交点横坐标就是对应的一元二次方程的根,而相应不等式可以根据函数值的正负来确定x的取值范围,二次函数是主干,一元二次方程和不等式就像它的两翼.(2)某网店销售一批新款削笔器,每个削笔器的最低售价为15元,若按最低售价销售,每天能卖出30个,若一个削笔器的售价每提高1元,日销售量将减少2个,为了使这批削笔器每天获得400元以上的销售收入,应怎样制定这批削笔器的销售价格?解:设这批削笔器每一个的销售价格为(),则每天销售量为设销售收入为,当时,得,,又所以.答:这批削笔器的销售价格应该定在.方法总结:设未知数,根据题意写出函数,不等式,求解实际问题.以二次函数为例为建立数学模型解决实际问题的学习打下基础.(3)当取何值时,一元不等式对一切实数都成立?解:①若,则即对一切实数都成立.②若,则二次函数的图像开口向上,函数值不可能恒为负数,对一切实数不可能恒成立.4③若,则二次函数的图像开口向下,函数值恒为负数时,函数图像和x轴无交点,即对一切实数恒成立时即解得:.综上所得:时,一元不等式对一切实数都成立.方法总结:关于x的含参的不等式,要关注二次项系数是否为0,根据函数的图像性质对不等式恒成立问题分类讨论.【活动预设】通过解题重新梳理二次函数与二次方程不等式的解的关系.老师...