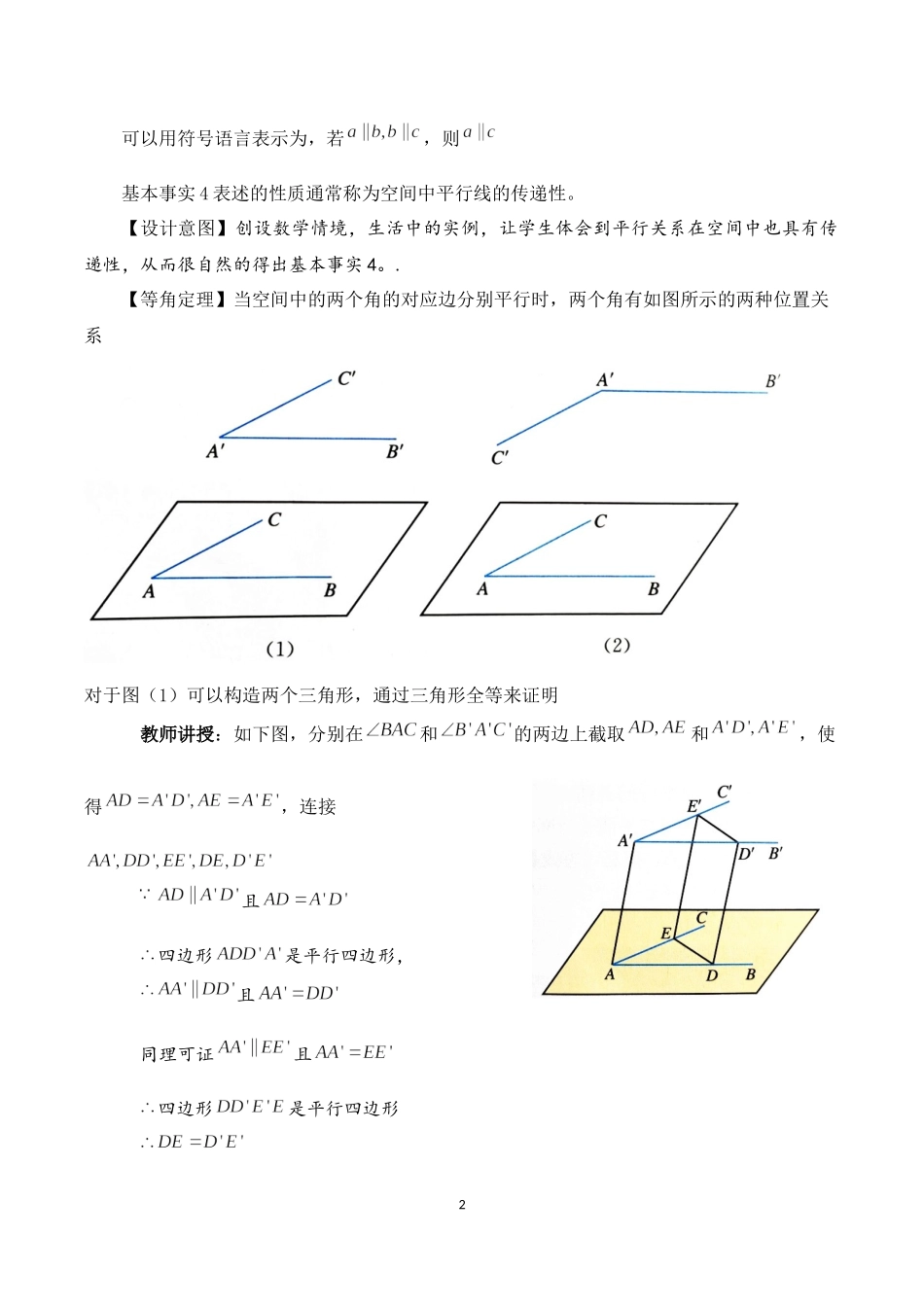
18.5.1直线与直线平行(人教A版普通高中教科书数学必修第二册第八章)深圳市第三高级中学张海娟一、教学目标1.理解基本事实4,会用基本事实4证明线线平行;2.掌握等角定理及其证明方法,能用等角定理求角度。二、教学重难点1.基本事实四,等角定理2.利用基本事实4证明线线平行三、教学过程1.情境引入1.1创设情境,引发思考【实际情境】在长方体中,,那么与平行吗?观察你所在的教室,你能找到实例吗?实际生活中还有没有这样的实例呢?问题1:在平面中平行线具有传递性,这个性质在空间中是否仍然成立?【预设的答案】仍然成立【设计意图】本节课的内容就是平面图形中的两个结论推广到空间图形中,平面图形的性质不一定能全部推广立体图形,一般来说,要把平面图形的结论推广到空间,要经过证明.问题2:在平面内,一个角的两边分别平行于另一个角的两边,则两个角相等或互补,在空间中,这一结论是否还成立呢?【活动预设】引导学生从已知到未知,由平面上的问题思考空间中的问题。1.2探究典例,形成概念【平行直线】基本事实4平行于同一条直线的两条直线相互平行。2可以用符号语言表示为,若,则基本事实4表述的性质通常称为空间中平行线的传递性。【设计意图】创设数学情境,生活中的实例,让学生体会到平行关系在空间中也具有传递性,从而很自然的得出基本事实4。.【等角定理】当空间中的两个角的对应边分别平行时,两个角有如图所示的两种位置关系对于图(1)可以构造两个三角形,通过三角形全等来证明教师讲授:如下图,分别在和的两边上截取和,使得,连接且四边形是平行四边形,且同理可证且四边形是平行四边形3【设计意图】证明空间中的等角定理,培养学生数学思维的严谨性.【等角定理】空间中如果两个角的两边分别对应平行,则这两个角相等或互补特别说明:若两个角的两边分别平行且方向相同,则两个角相等;如果两边分别平行,且一边方向相同,另一边方向相反,则这两个角互补。1.3具体感知,理性分析例1、已知是四个顶点不在同一个平面内的空间四边形,分别是的中点,连接,求证四边形是一个平行四边形。思考:在例1中,如果再加上,那么四边形是什么图形?【设计意图】基本事实4的一个简单应用,考察学生的空间想象能力和空间中平行线传递性的理解.练习如图,四边形ABEF和四边形ABCD都是直角梯形,且,且,分别为的中点。(1)证明:四边形BCHG是平行四边形。(2)C,D,F,E四点是否共面?为什么?42.初步应用,理解概念1下列结论中正...