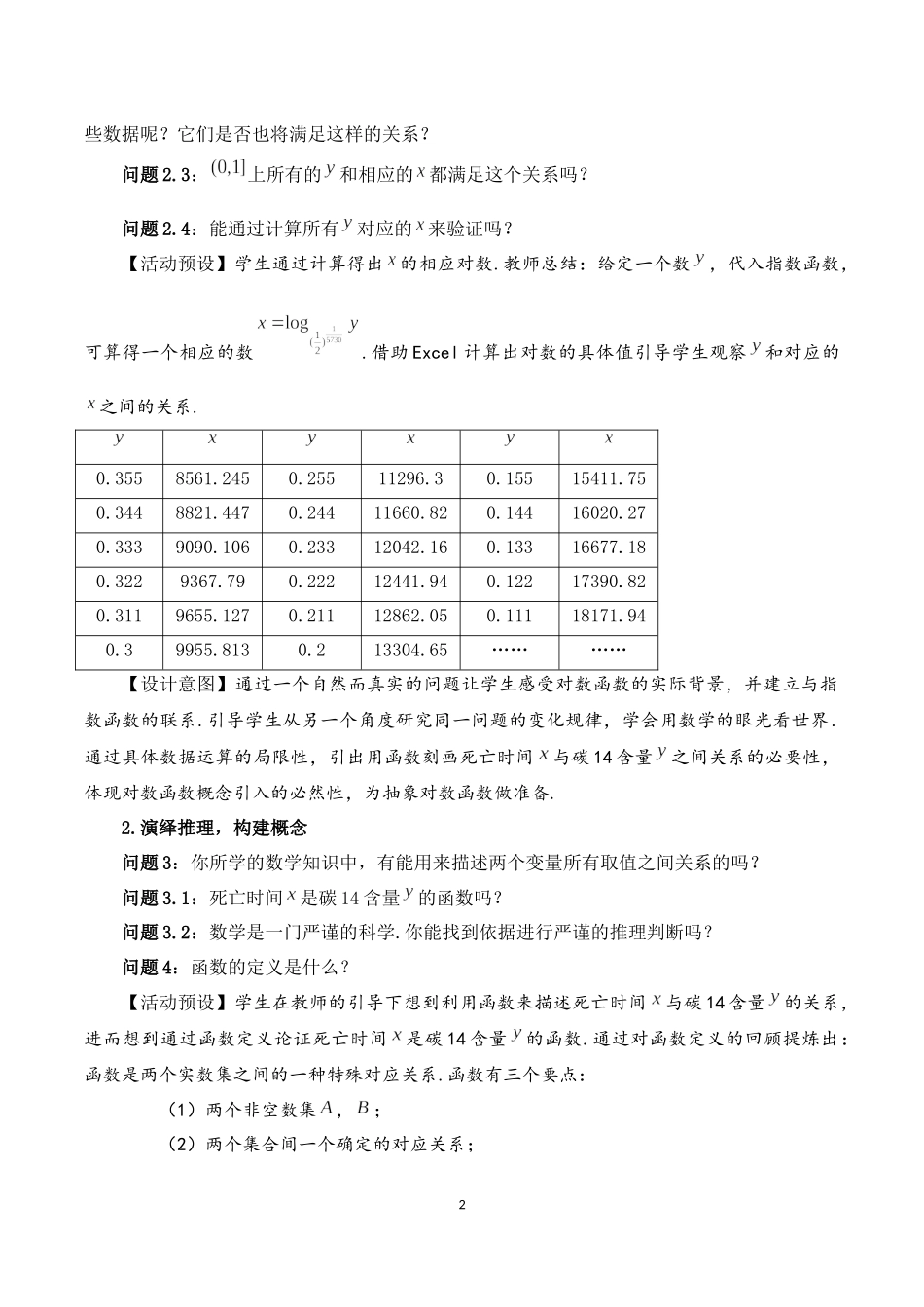
14.4.1对数函数的概念(第一课时)(人教A版普通高中教科书数学必修第一册第四章)宝安中学李晶一、教学目标1.通过解决具体实例中的指数函数已知,求问题,感受对数函数的实际背景,感悟对数函数概念引入的必然性,夯实提出问题、分析问题、解决问题的学习力.2.通过经历对数函数概念的构建过程,让学生感悟研究函数的方法,理解对数函数的概念,体会数形结合、类比、特殊到一般,具体到抽象的数学思想,促进演绎、归纳法的内化,渗透逻辑推理、数学抽象、直观想象的核心素养.3.通过应用,掌握对数函数解析式及对数型函数定义域求解;感悟指数、对数函数是从不同角度研究同一类问题变化规律两大基本初等函数,渗透数学建模、数学运算核心素养.二、教学重难点1.对数函数的概念;.2.利用函数定义,演绎推理对数函数的概念三、教学过程1.创设情境,引发思考【实际情境】在周末参观古生物博物馆时,孩子看着恐龙化石提了一个问题:“我们怎么知道霸王龙是生活在白垩纪,而不是侏罗纪呢?”同学们,你们能回答这个问题吗?考古学家是如何利用遗址中的化石,推断恐龙生活的年代的呢?【预设的答案】通过测定化石碳14含量来推算化石年代,师生一起复习碳14指数函数.问题1:考古学家反过来利用这个函数来推算化石年代,他们是如何操作的呢?问题2:如果已测得为,,,那么相应的分别为多少?问题2.1:的相应对数代表多少年呢?问题2.2:从这3组数中可以直观感受到:碳14含量越小,死亡时间就越大.再多一2些数据呢?它们是否也将满足这样的关系?问题2.3:上所有的和相应的都满足这个关系吗?问题2.4:能通过计算所有对应的来验证吗?【活动预设】学生通过计算得出的相应对数.教师总结:给定一个数,代入指数函数,可算得一个相应的数.借助Excel计算出对数的具体值引导学生观察和对应的之间的关系.0.3558561.2450.25511296.30.15515411.750.3448821.4470.24411660.820.14416020.270.3339090.1060.23312042.160.13316677.180.3229367.790.22212441.940.12217390.820.3119655.1270.21112862.050.11118171.940.39955.8130.213304.65…………【设计意图】通过一个自然而真实的问题让学生感受对数函数的实际背景,并建立与指数函数的联系.引导学生从另一个角度研究同一问题的变化规律,学会用数学的眼光看世界.通过具体数据运算的局限性,引出用函数刻画死亡时间与碳14含量之间关系的必要性,体现对数函数概念引入的必然性,为抽象对数函数做准备.2.演绎推理,构建...