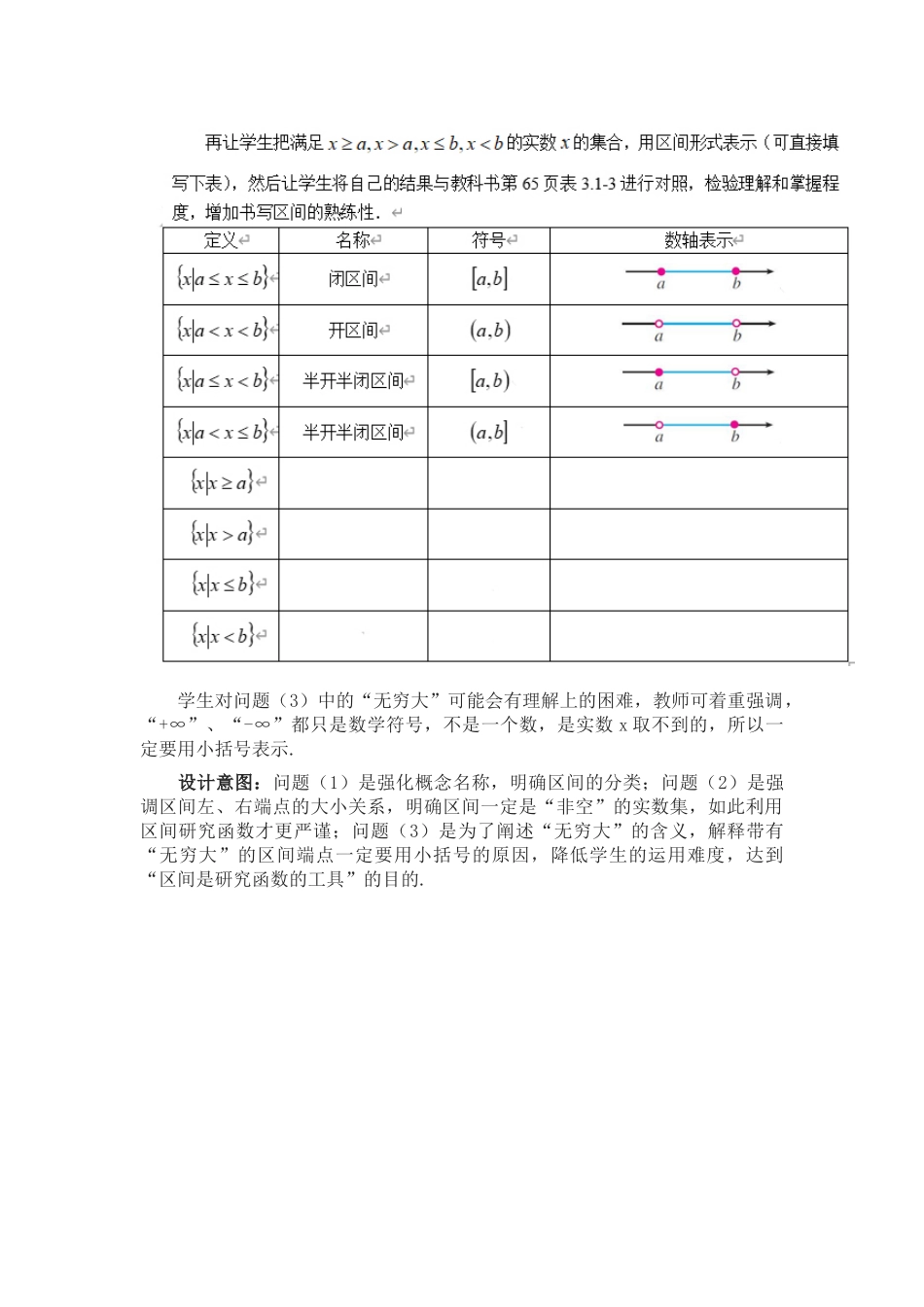
3.1.1函数的概念(第2课时)(人教A版普通高中教科书数学必修第一册第三章)人大附中深圳中学王欢庆一、教学目标1、理解区间的概念,“开”、“闭”的含义,及“∞”、“+∞”、“-∞”的读法与含义,掌握满足相应不等式条件的实数x的集合与区间之间的相互转化.2、了解构成函数的要素,能够正确说出函数的三要素,会求一些简单函数的定义域.3、会判断两个函数是否为同一函数,理解定义域对函数的限定性作用.二、教学重难点1、函数定义域的求法。2、如何判断两个函数为同一函数.三、教学过程(一)区间概念的引入问题1:由上节课的学习我们知道,函数的三要素为定义域、对应关系和值域,定义域和值域都是非空数集.在数学中有没有刻画非空数集的简单方式呢?请大家阅读教科书第64页相关内容.(1)什么叫闭区间?什么叫开区间?什么叫半开半闭区间?(2)区间的端点应满足什么条件?0(3)请用区间表示实数集R。书写带有“+∞”、“-∞”的区间时,应使用小括号还是中括号?师生活动:教师先让学生阅读并独立思考,尝试理解有关概念和相应记法,然后提出上述3个问题,检验学生自主阅读和理解能力,并提醒学生先不要看教科书第65页.学生对问题(3)中的“无穷大”可能会有理解上的困难,教师可着重强调,“+∞”、“-∞”都只是数学符号,不是一个数,是实数x取不到的,所以一定要用小括号表示.设计意图:问题(1)是强化概念名称,明确区间的分类;问题(2)是强调区间左、右端点的大小关系,明确区间一定是“非空”的实数集,如此利用区间研究函数才更严谨;问题(3)是为了阐述“无穷大”的含义,解释带有“无穷大”的区间端点一定要用小括号的原因,降低学生的运用难度,达到“区间是研究函数的工具”的目的.设计意图:问题(1)是引导学生思考给定解析式后,求定义域的原则;并通过具体实例进行操作,熟悉求解过程;熟练具体区间的书写,并明确区间的交并运算符号与集合完全一致(因为区间是集合的一种特殊形式).师生活动:教师用PPT或其他方式呈现问题3,给学生适当时间计算,然后找同学公布答案,必要时给予适当修正.追问:通过问题2和问题3,你能总结函数定义域的常用求法吗?给学生适当时间思考,然后提问一名同学,视情况找其他同学补充,最终达成共识:①负数不能开平方(基础稍好的学生也可总结出:负数不能开偶次方);②分母不能为零;③有限个函数的四则运算得到的新函数,它的定义域是这有限个函数定义域的交集.设计意图:通过具体实例...