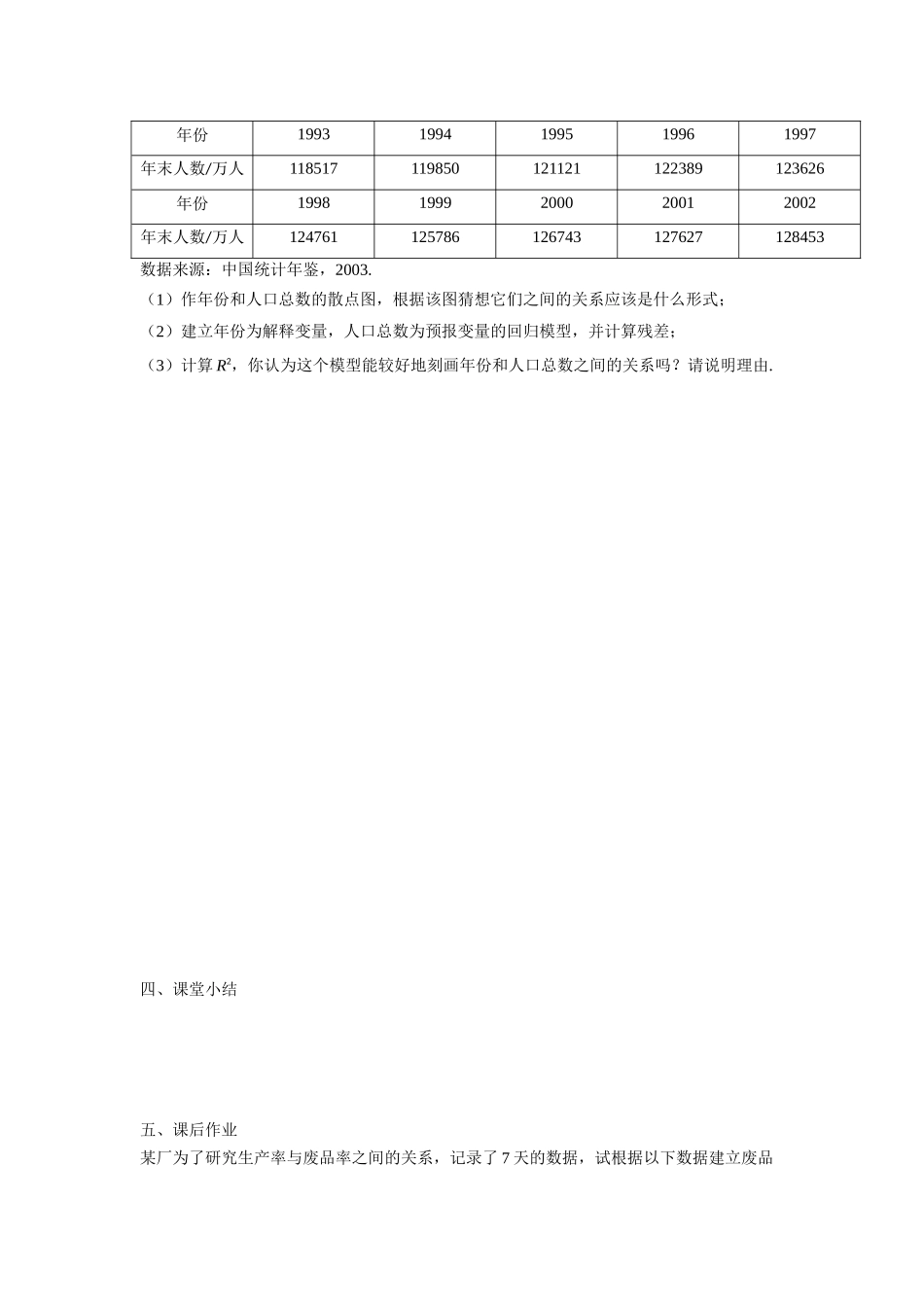
《回归分析的基本思想及其初步应用(2)》学习任务单教学目标1.了解回归分析的基本思想方法及其简单应用,明确建立回归模型的基本步骤.2.了解残差分析和指标R2,会初步应用.3.通过本节课的学习,培养应用意识,提升发现问题、解决问题的能力.教学重点、难点1.教学重点:残差分析和指标R2.2.教学难点:利用残差和指标R2分析回归模型的拟合效果.课上任务一、复习回顾通过上节课的实例分析,我们对回归分析的基本思想及其应用有了初步的认识,那么结合实例请同学们回顾所学知识:1.判断两个变量线性相关的方法.2.回归方程的求法.3.利用回归方程进行预测.4.随机误差.5.线性回归模型的完整表达式.6.产生随机误差项e的原因.二、讲授新课(一)概念1.残差:2.指标R2:(二)探究探究1:我们如何通过残差来分析模型的拟合效果呢?探究2:通过残差表或残差图判断模型拟合的效果是直观判断,如何精确判断模型拟合的效果呢?探究3:相关系数r与指标R2间有什么关系呢?探究4:用身高预报体重需要注意哪些问题?探究5:你能总结出建立回归模型的基本步骤吗?三、典例分析例.1993年至2002年每年中国人口总数的数据如下表:年份19931994199519961997年末人数/万人118517119850121121122389123626年份19981999200020012002年末人数/万人124761125786126743127627128453数据来源:中国统计年鉴,2003.(1)作年份和人口总数的散点图,根据该图猜想它们之间的关系应该是什么形式;(2)建立年份为解释变量,人口总数为预报变量的回归模型,并计算残差;(3)计算R2,你认为这个模型能较好地刻画年份和人口总数之间的关系吗?请说明理由.四、课堂小结五、课后作业某厂为了研究生产率与废品率之间的关系,记录了7天的数据,试根据以下数据建立废品率与生产率的回归模型.生产率/(个•天-1)1000200030003500400045005000废品率/%5.26.56.88.110.210.313(1)作生产率和废品率的散点图,根据该图猜想它们之间的关系应该是什么形式;(2)建立生产率为解释变量,废品率为预报变量的回归模型,并计算残差;(3)计算R2,你认为这个模型能较好地刻画生产率和废品率之间的关系吗?请说明理由.作业答案(1)线性相关关系;500100015002000250030003500400045005000550002468101214生产率/%废品率/(个·天-1)(2);(3)略.