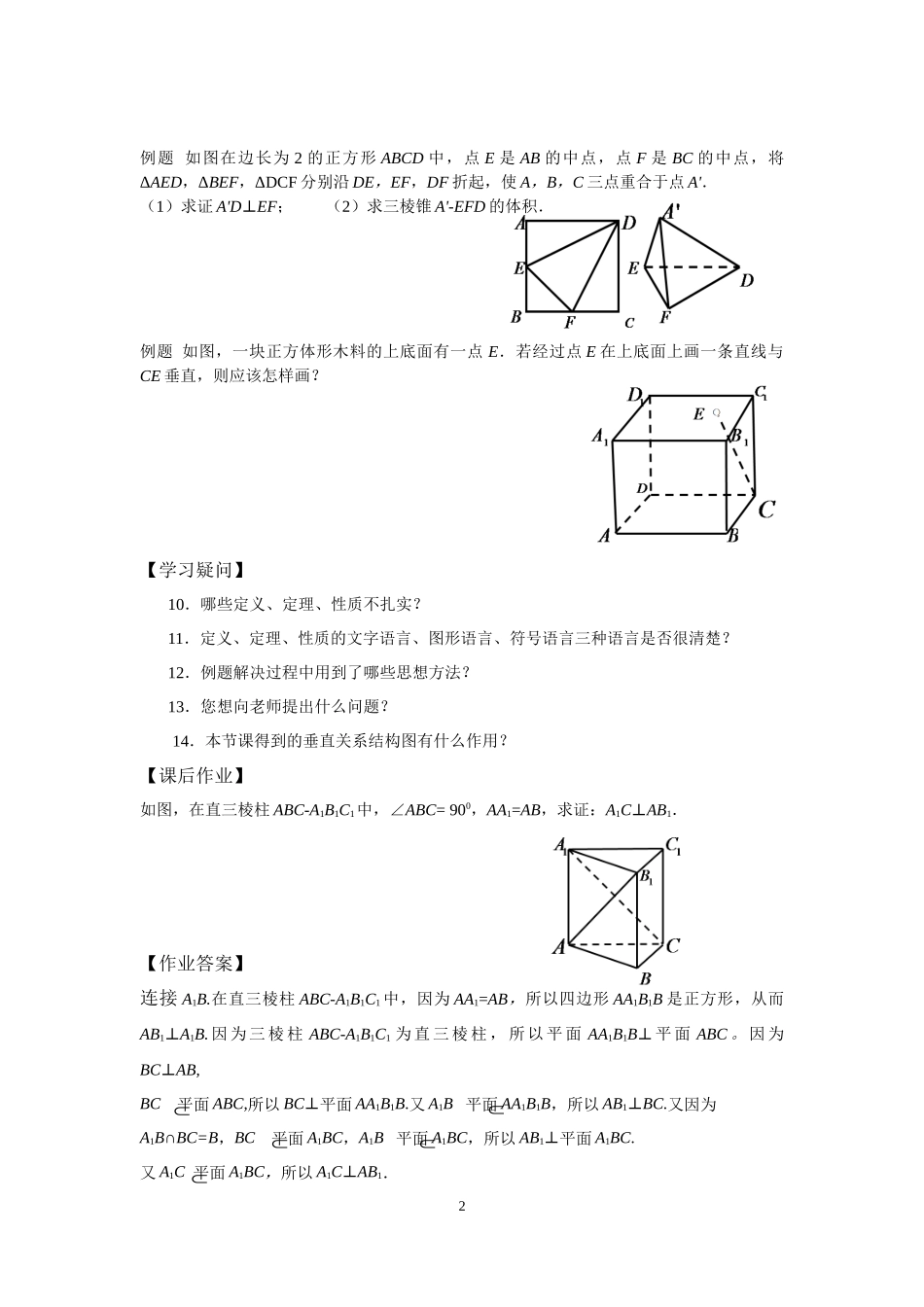
1《空间立体几何初步单元复习(第三课时)》学习任务单【学习目标】本节课是对本章内容涉及到的立体几何中的垂直关系进行复习总结,能把定义、定理用三种符号语言灵活的表达出来,理解直线与直线、直线与平面、平面与平面垂直的相互转化,能运用有关定理或性质证明直线、平面之间的垂直关系.【课上任务】一.知识梳理1.直线与直线垂直的定义是什么?空间中直线与直线垂直包括共面垂直和异面垂直,常用证明方法是什么?2.直线与平面垂直的定义是什么?定义中需注意什么?3.由直线与平面垂直的定义得到经常使用的命题是什么?4.直线与平面垂直判定定理是什么?定理中需注意什么?5.判定直线与平面垂直常用命题是什么?6.直线与平面垂直的性质是什么?7.平面与平面垂直的定义是什么?8.平面与平面垂直的判定定理是什么?9.平面与平面垂直的性质定理是什么?关键条件是什么?A.充分不必要条件B.必要不充分条件C.充要条件D.既不充分也不必要条件例题下列命题中正确的是_____________.①垂直于同一直线的两条直线平行②垂直于同一平面的两个平面平行③垂直于同一平面的两条直线平行④垂直于同一直线的两个平面平行例题如图AB是的直径,点C是上的动点,过动点C的直线VC垂直于所在的平面,D,E分别是VA,VC的中点.判断直线DE与平面VBC的位置关系,并说明理由.OOO二、例题解析例题设l,m,n均为直线,其中m,n在平面α内,则“lα”⊥是“l⊥m,l⊥n”的().2例题如图在边长为2的正方形ABCD中,点E是AB的中点,点F是BC的中点,将ΔAED,ΔBEF,ΔDCF分别沿DE,EF,DF折起,使A,B,C三点重合于点A'.(1)求证A'D⊥EF;(2)求三棱锥A'-EFD的体积.例题如图,一块正方体形木料的上底面有一点E.若经过点E在上底面上画一条直线与CE垂直,则应该怎样画?【学习疑问】10.哪些定义、定理、性质不扎实?11.定义、定理、性质的文字语言、图形语言、符号语言三种语言是否很清楚?12.例题解决过程中用到了哪些思想方法?13.您想向老师提出什么问题?14.本节课得到的垂直关系结构图有什么作用?【课后作业】如图,在直三棱柱ABC-A1B1C1中,∠ABC=900,AA1=AB,求证:A1C⊥AB1.【作业答案】连接A1B.在直三棱柱ABC-A1B1C1中,因为AA1=AB,所以四边形AA1B1B是正方形,从而AB1⊥A1B.因为三棱柱ABC-A1B1C1为直三棱柱,所以平面AA1B1B⊥平面ABC。因为BC⊥AB,BC平面ABC,所以BC⊥平面AA1B1B.又A1B平面AA1B1B,所以AB1⊥BC.又因为A1B∩BC=B,BC平面A1BC,A1B平面A1BC,所以AB1⊥平面A1BC.又A1C平面A1BC,所以A1C⊥AB1.