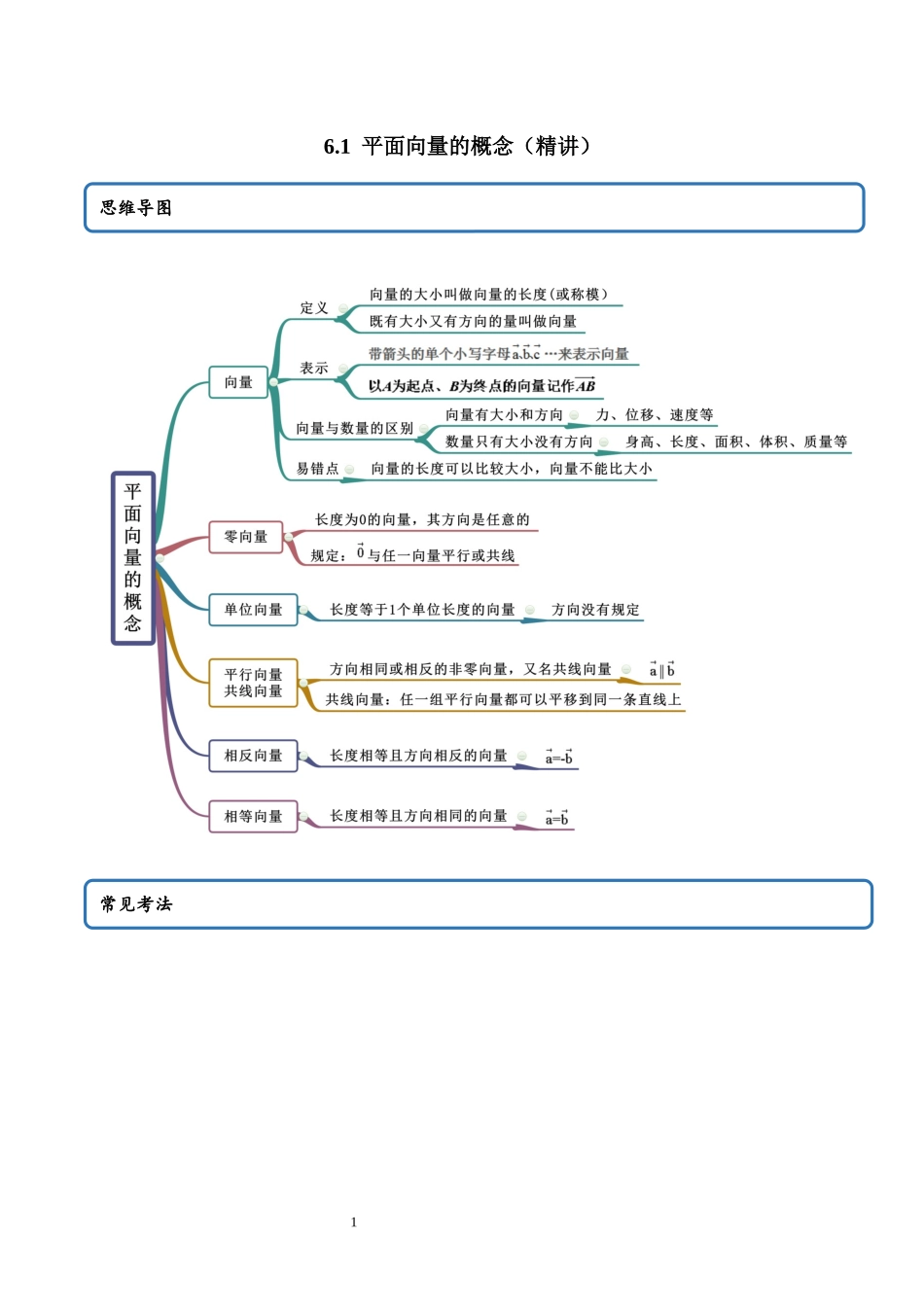
16.1平面向量的概念(精讲)思维导图常见考法2考法一向量与数量的区别【例1】(2020·全国高一)下列各量中是向量的是()A.时间B.速度C.面积D.长度【答案】B【解析】既有大小,又有方向的量叫做向量;时间、面积、长度只有大小没有方向,因此不是向量.而速度既有大小,又有方向,因此速度是向量.故选:.【跟踪训练】1.(2020·全国高一课时练习)下列量不是向量的是()A.力B.速度C.质量D.加速度【答案】C【解析】质量只有大小,没有方向,不是向量.故选C2.(2020·全国高一课时练习)给出下列物理量:①密度;②路程;③速度;④质量;⑤功;⑥位移.下列说法正确的是()A.①②③是数量,④⑤⑥是向量B.②④⑥是数量,①③⑤是向量C.①④是数量,②③⑤⑥是向量D.①②④⑤是数量,③⑥是向量【答案】D【解析】【解析】由物理知识可知,密度,路程,质量,功只有大小,没有方向,因此是数量而速度,位移既有大小又有方向,因此是向量.故选:D3.(2020·全国高一课时练习)下列说法正确的是()A.数量可以比较大小,向量也可以比较大小B.方向不同的向量不能比较大小,但同向的可以比较大小C.向量的大小与方向有关D.向量的模可以比较大小3【答案】D【解析】向量不能比较大小,向量的模能比较大小,显然D正确.考法二向量的几何表示【例2】(2020·全国高一专题练习)某人从A点出发向东走了5米到达B点,然后改变方向沿东北方向走了米到达C点,到达C点后又改变方向向西走了10米到达D点.(1)作出向量,,;(2)求的模.【答案】(1)见解析;(2)米【解析】(1)作出向量,,;如图所示:(2)由题意得,△BCD是直角三角形,其中∠BDC=90°,BC=10米,CD=10米,所以BD=10米.△ABD是直角三角形,其中∠ABD=90°,AB=5米,BD=10米,所以AD==(米),所以|米.【跟踪训练】1.(2021·江苏高一)如图的方格由若干个边长为1的小正方形组成,方格中有定点A,点C为小正方形的顶点,且,画出所有的向量.4【答案】见解析【解析】 ,∴C点落在以A为圆心,以为半径的圆上,又 点C为小正方形的顶点,根据该条件不难找出满足条件的点C,解析所有的向量,如图所示:2.(2020·全国高一课时练习)在如图所示的坐标纸(规定小方格的边长为1)中,用直尺和圆规画出下列向量:5(1),点A在点O正南方向;(2),点B在点O北偏西方向;(3),点C在点O南偏西方向.【答案】(1)作图见解析(2)作图见解析(3)作图见解析【解析】如图.3.(202...