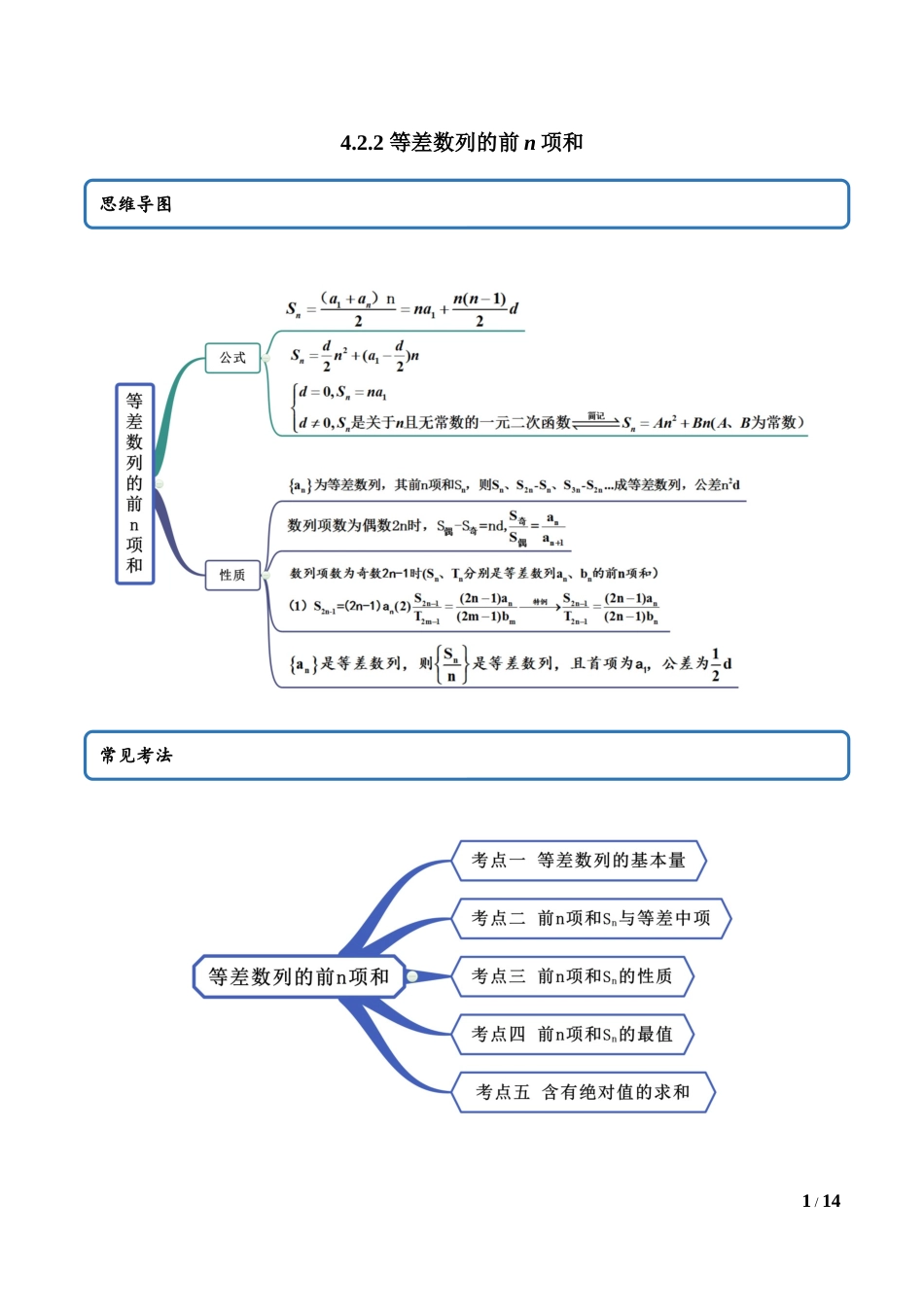
1/144.2.2等差数列的前n项和思维导图常见考法2/14考点一等差数列的基本量【例1】(2020·陕西省安康中学其他(理))记为等差数列的前项和,,,则()A.-77B.-70C.-49D.-42【答案】A【解析】由,得,∴,,.故选:A【一隅三反】1.(2020·内蒙古赤峰)若等差数列的前项和为,且满足,,则公差()A.1B.C.2D.【答案】A【解析】 ,∴,,解得.故选:A.2.(2020·河南信阳·其他(文))正项等差数列的前和为,已知,则=()A.35B.36C.45D.54【答案】C【解析】正项等差数列的前项和,,,解得或(舍),,故选C.3.(2020·湖北十堰)已知等差数列的前n项和满足,则()A.12B.13C.14D.15【答案】D3/14【解析】因为,所以,又,所以.故,解得.故选:D.考点二前n项和Sn与等差中项【例2】(1)(2020·云南省云天化中学高一期末)等差数列中,,则数列前11项和()A.12B.60C.66D.72(2).(2020·吉林朝阳·长春外国语学校开学考试)设是等差数列的前n项和,若则()A.B.C.D.【答案】(1)C(2)A【解析】(1)在等差数列中,,所以所以.故选:C.(2)在等差数列{an}中,由,得故选:A4/14【一隅三反】1.(2020·四川成都·二模(文))若数列为等差数列,且满足,为数列的前项和,则()A.B.C.D.【答案】B【解析】因为,由等差数列性质,若,则得,.为数列的前项和,则.故选:.2.(2020·河北运河·沧州市一中月考)若两个等差数列的前n项和分别为,,且满足,则()A.2B.C.D.【答案】D【解析】,又因为,所以.故选:D(1)如果为等差数列,若,则.(2)要注意等差数列前项和公式的灵活应用,如.5/143.(2020·河北新华·石家庄新世纪外国语学校期中)两等差数列和,前n项和分别为,,且,则的值为()A.B.C.D.【答案】A【解析】在为等差数列中,当,,,时,.所以,又因为,所以.故选:A.4.(2020·湖南宁乡一中)在等差数列中,,则此数列前项的和是().A.B.C.D.【答案】B【解析】由等差数列的性质可得:,,代入已知可得,即,故数列的前项之和.故选.考点三前n项和Sn的性质【例3】(1)(2020·陕西省洛南中学高二月考)已知某等差数列共有10项,其奇数项之和为15,偶数项之和为30,则其公差为()A.6B.5C.4D.36/14(2).(2019·陕西武功·高三月考(理))设等差数列的前项和为若,,则()A.45B.54C.72D.81(3)(2020·浙江吴兴·湖州中学)设为等差数列的前项和,且,,则()A.B...