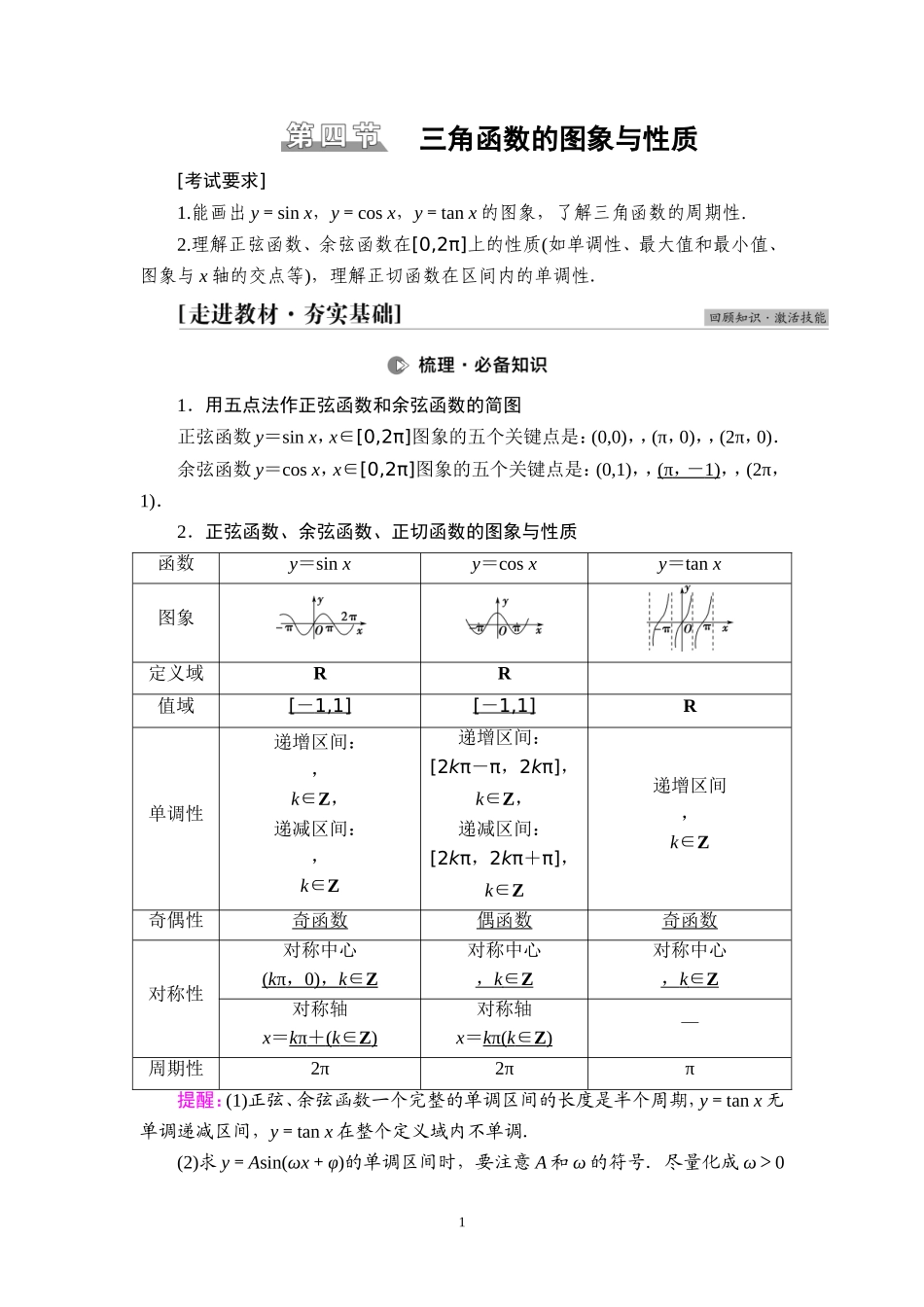
三角函数的图象与性质[考试要求]1.能画出y=sinx,y=cosx,y=tanx的图象,了解三角函数的周期性.2.理解正弦函数、余弦函数在[0,2π]上的性质(如单调性、最大值和最小值、图象与x轴的交点等),理解正切函数在区间内的单调性.1.用五点法作正弦函数和余弦函数的简图正弦函数y=sinx,x∈[0,2π]图象的五个关键点是:(0,0),,(π,0),,(2π,0).余弦函数y=cosx,x∈[0,2π]图象的五个关键点是:(0,1),,(π,-1),,(2π,1).2.正弦函数、余弦函数、正切函数的图象与性质函数y=sinxy=cosxy=tanx图象定义域RR值域[-1,1][-1,1]R单调性递增区间:,k∈Z,递减区间:,k∈Z递增区间:[2kπ-π,2kπ],k∈Z,递减区间:[2kπ,2kπ+π],k∈Z递增区间,k∈Z奇偶性奇函数偶函数奇函数对称性对称中心(kπ,0),k∈Z对称中心,k∈Z对称中心,k∈Z对称轴x=kπ+(k∈Z)对称轴x=kπ(k∈Z)—周期性2π2ππ提醒:(1)正弦、余弦函数一个完整的单调区间的长度是半个周期,y=tanx无单调递减区间,y=tanx在整个定义域内不单调.(2)求y=Asin(ωx+φ)的单调区间时,要注意A和ω的符号.尽量化成ω>01的形式,避免出现增减区间的混淆.1.对称与周期(1)正弦曲线、余弦曲线相邻两对称中心、相邻两对称轴之间的距离是半个周期,相邻的对称中心与对称轴之间的距离是个周期.(2)正切曲线相邻两对称中心之间的距离是半个周期.2.函数具有奇、偶性的充要条件(1)函数y=Asin(ωx+φ)(x∈R)是奇函数⇔φ=kπ(k∈Z);(2)函数y=Asin(ωx+φ)(x∈R)是偶函数⇔φ=kπ+(k∈Z);(3)函数y=Acos(ωx+φ)(x∈R)是奇函数⇔φ=kπ+(k∈Z);(4)函数y=Acos(ωx+φ)(x∈R)是偶函数⇔φ=kπ(k∈Z).一、易错易误辨析(正确的打“√”,错误的打“×”)(1)正切函数y=tanx在定义域内是增函数.()(2)已知y=ksinx+1,x∈R,则y的最大值为k+1.()(3)函数y=sinx的图象关于点(kπ,0)(k∈Z)中心对称.()(4)y=sin|x|与y=|sinx|都是周期函数.()[答案](1)×(2)×(3)√(4)×二、教材习题衍生1.若函数y=2sin2x-1的最小正周期为T,最大值为A,则()A.T=π,A=1B.T=2π,A=1C.T=π,A=2D.T=2π,A=2A[T==π,A=2-1=1,故选A.]2.函数y=tan2x的定义域是()A.B.C.D.D[由2x≠kπ+,k∈Z,得x≠+,k∈Z,∴y=tan2x的定义域为.]3.y=sin的单调递减区间是________.(k∈Z)[由+2kπ≤2x-≤+2kπ,k∈Z得,+kπ≤x≤+kπ,k∈Z.]4.函数y=...