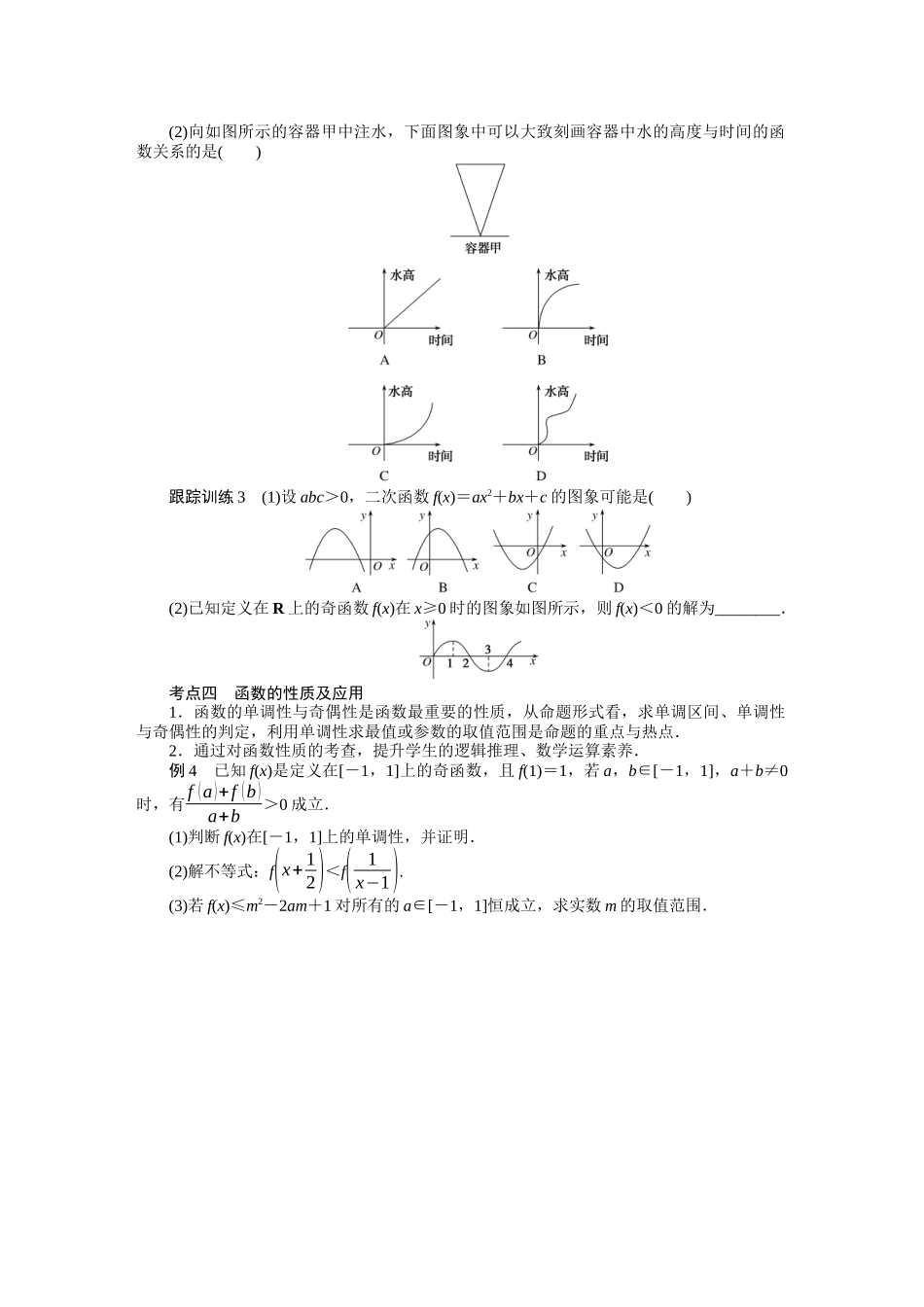
专项培优③考点一函数的概念与表示1.定义域、对应关系和值域是函数的三个不可分割的要素,其中定义域和对应关系是最本质的要素,这两个确定了,值域也就确定了.2.通过对函数的概念与表示的考查,提升学生的逻辑推理、数学运算素养.例1(1)函数f(x)=2x2√1−x+(2x-1)0的定义域为()A.(-∞,12)B.(12,1)C.(−12,12)D.(−∞,12)∪(12,1)(2)已知a,b为常数,且a≠0,f(x)=ax2+bx,f(2)=0,方程f(x)=x有两个相等的实数根.①求函数f(x)的解析式;②当x∈[1,2]时,求f(x)的值域.跟踪训练1(1)函数y=√7+6x−x2的定义域是________.(2)函数f(x)在R上为奇函数,当x>0时,f(x)=√x+1,则f(x)的解析式为________.考点二分段函数1.分段函数在定义域的不同部分上有不同的表达式,主要考查与分段函数有关的求值、求参数、单调性、奇偶性等问题.2.通过对分段函数的考查,提升学生的数学运算素养.例2已知函数f(x)={12x,0<x<1,34−x4,1≤x<2,54−12x,2≤x<52.(1)求f(x)的定义域、值域;(2)求f(f(1));(3)解不等式f(x+1)>14.跟踪训练2设f(x)={√x,0<x<1,2(x−1),x≥1,若f(a)=f(a+1),则f(1a)=()A.2B.4C.6D.8考点三函数的图象及应用1.函数的图象是函数的重要表示方法,它具有明显的直观性,通过函数的图象能够掌握函数重要的性质,如单调性、奇偶性等.反之,掌握好函数的性质,有助于图象正确的画出.函数图象广泛应用于解题过程中,利用数形结合解题具有直观、明了、易懂的优点,在历届高考试题中,常出现有关函数图象和利用图象解题的试题.2.通过对函数图象的考查,提升学生的直观想象、逻辑推理素养.例3(1)函数f(x)=ax+b(x+c)2的图象如图所示,则下列结论成立的是()A.a>0,b>0,c<0B.a<0,b>0,c>0C.a<0,b>0,c<0D.a<0,b<0,c<0(2)向如图所示的容器甲中注水,下面图象中可以大致刻画容器中水的高度与时间的函数关系的是()跟踪训练3(1)设abc>0,二次函数f(x)=ax2+bx+c的图象可能是()(2)已知定义在R上的奇函数f(x)在x≥0时的图象如图所示,则f(x)<0的解为________.考点四函数的性质及应用1.函数的单调性与奇偶性是函数最重要的性质,从命题形式看,求单调区间、单调性与奇偶性的判定,利用单调性求最值或参数的取值范围是命题的重点与热点.2.通过对函数性质的考查,提升学生的逻辑推理、数学运算素养.例4已知f(x)是定义在[-1,1]上的奇函数,且f(1)=1,若a,b∈[-1,1]...