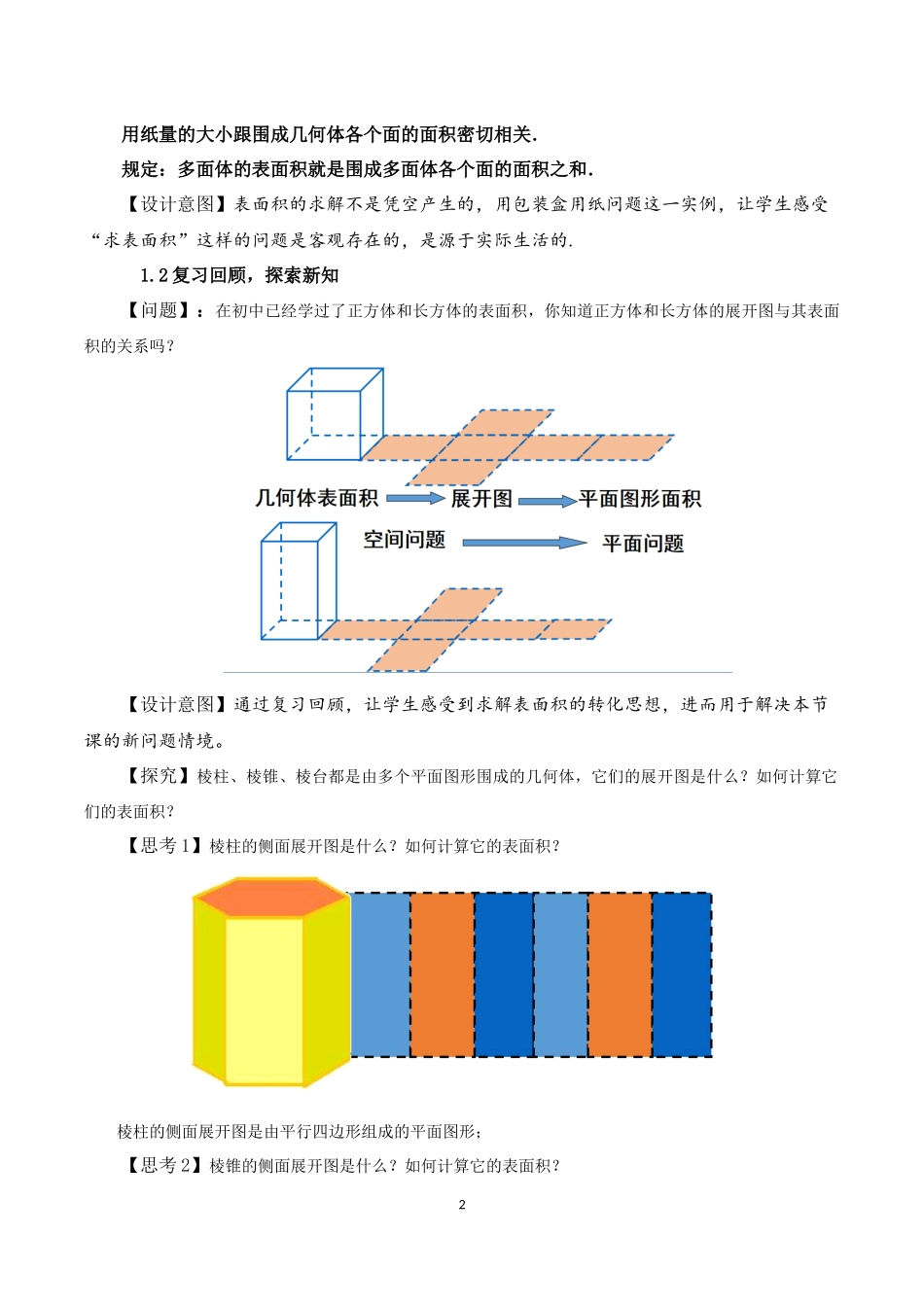
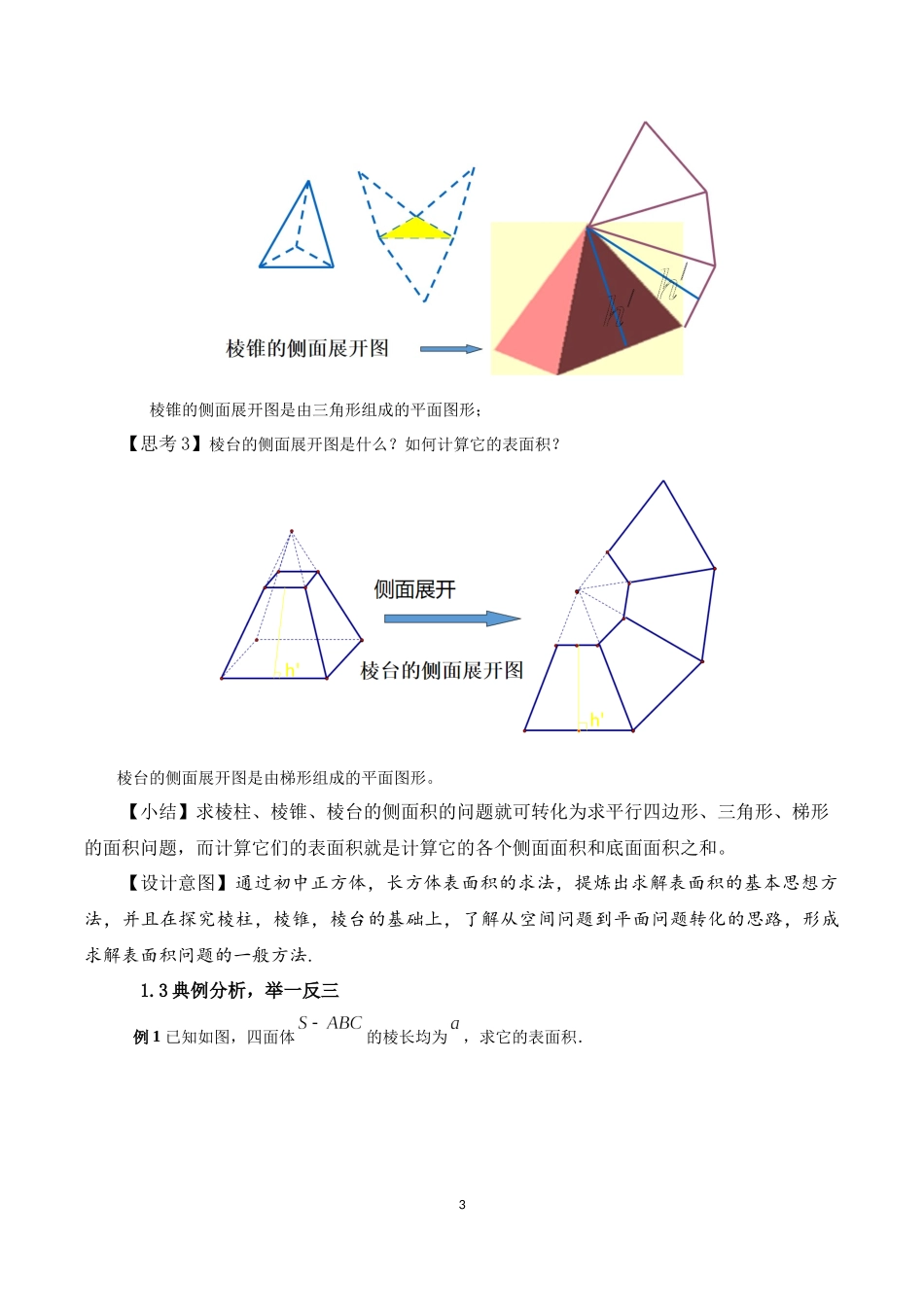
18.3.1棱柱、棱锥、棱台的表面积和体积(人教A版普通高中教科书数学必修第二册第八章)深圳市第七高级中学游云峰本节课选自《普通高中课程标准数学教科书-必修第二册》(人教A版)第八章《立体几何初步》,本节课主要学习棱柱、棱锥、棱台的表面积和体积的表面积、体积公式及其求法,还有简单组合体的体积的求解。教材从分析简单几何体的侧面展开图得到了它们的表面积公式,体现了立体问题平面化的解决策略,这是本节课的灵魂,也是立体几何的灵魂,在立体几何中,要注意将立体问题转化为平面几何问题,在教学中应加以重视。一、教学目标与数学学科素养课程目标1.通过对棱柱、棱锥、棱台的研究,掌握棱柱、棱锥、棱台的表面积和体积计算公式.2.能运用棱柱、棱锥、棱台的表面积和体积公式进行计算和解决有关实际问题.数学学科素养1.数学抽象:棱柱、棱锥、棱台的体积公式;2.数学运算:求多面体或多面体组合体的表面积和体积;3.数学建模:数形结合,运用棱柱、棱锥、棱台的表面积和体积公式进行计算和解决有关实际问题.二、教学重难点1.教学重点:棱柱、棱锥、棱台的表面积与体积;2.教学难点:求棱柱、棱锥、棱台有关的组合体的表面积与体积.三、教学过程1.表面积1.1创设情境,引入课题【实际情境】在生产生活中,会遇到包装盒用纸量的计算问题2用纸量的大小跟围成几何体各个面的面积密切相关.规定:多面体的表面积就是围成多面体各个面的面积之和.【设计意图】表面积的求解不是凭空产生的,用包装盒用纸问题这一实例,让学生感受“求表面积”这样的问题是客观存在的,是源于实际生活的.1.2复习回顾,探索新知【问题】:在初中已经学过了正方体和长方体的表面积,你知道正方体和长方体的展开图与其表面积的关系吗?【设计意图】通过复习回顾,让学生感受到求解表面积的转化思想,进而用于解决本节课的新问题情境。【探究】棱柱、棱锥、棱台都是由多个平面图形围成的几何体,它们的展开图是什么?如何计算它们的表面积?【思考1】棱柱的侧面展开图是什么?如何计算它的表面积?棱柱的侧面展开图是由平行四边形组成的平面图形;【思考2】棱锥的侧面展开图是什么?如何计算它的表面积?3棱锥的侧面展开图是由三角形组成的平面图形;【思考3】棱台的侧面展开图是什么?如何计算它的表面积?棱台的侧面展开图是由梯形组成的平面图形。【小结】求棱柱、棱锥、棱台的侧面积的问题就可转化为求平行四边形、三角形、梯形的面积问题,而计算它们的表面...