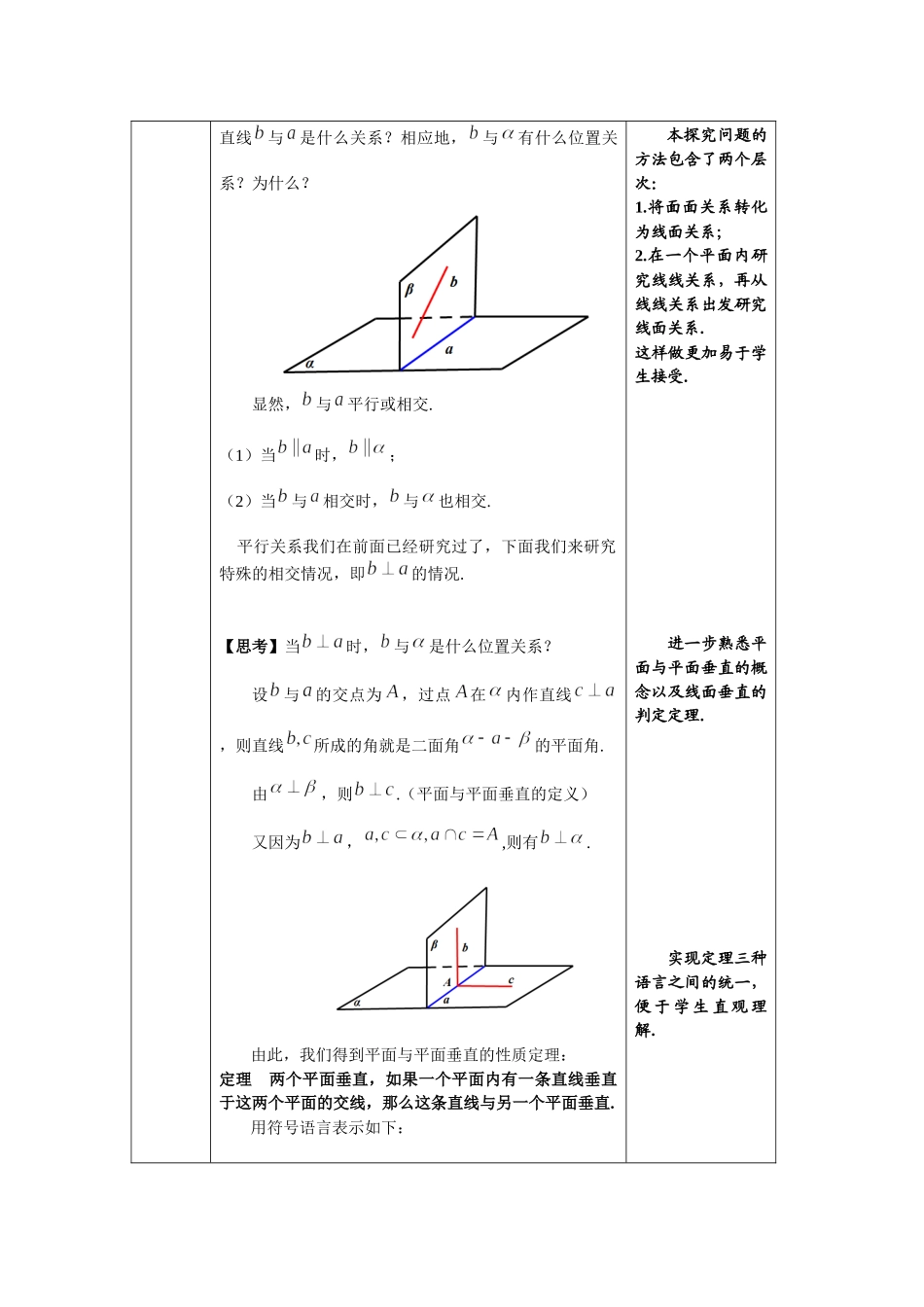
教案教学基本信息课题平面与平面垂直性质及应用学科数学学段:高一年级高一教材书名:普通高中教科书数学必修第二册出版社:人民教育出版社出版日期:2019年6月姓名单位设计者陈义明北京市顺义牛栏山第一中学实施者陈义明北京市顺义牛栏山第一中学指导者孙枫李淑敬、赵贺北京市顺义牛栏山第一中学北京市顺义区教育研究和教师研修中心课件制作者陈义明北京市顺义牛栏山第一中学其他参与者教学目标及教学重点、难点本节课主要掌握平面与平面垂直的性质定理并能够初步运用性质定理解决问题;对“垂直”关系进行梳理,理解直线与直线垂直、直线与平面垂直、平面与平面垂直的判定与性质之间的关系,体会“降维”思想在立体几何中的应用.教学过程中重点关注学生直观想象、逻辑推理能力的发展.教学过程(表格描述)教学环节主要教学活动设置意图引入前面我们研究了平面与平面垂直的判定,下面我们来研究平面与平面垂直的性质.也就是在两个平面互相垂直的条件下,能推出哪些结论.如果两个平面互相垂直,根据以往的研究经验,我们从哪儿入手开始研究呢?我们可以先研究一个平面内的直线与另一个平面具有怎样的位置关系.平面与平面垂直的判定与性质是我们研究的两个方面,性质的出发点是已知两个平面垂直,那么按照立体几何中“降维”的思想,很自然想到可以从“直线与平面”的位置关系入手进行研究.新课【探究】如图,设.则内任意一条直线与是什么关系?相应地,与有什么位置关系?为什么?显然,与平行或相交.(1)当时,;(2)当与相交时,与也相交.平行关系我们在前面已经研究过了,下面我们来研究特殊的相交情况,即的情况.【思考】当时,与是什么位置关系?设与的交点为,过点在内作直线,则直线所成的角就是二面角的平面角.由,则.(平面与平面垂直的定义)又因为,,则有.由此,我们得到平面与平面垂直的性质定理:定理两个平面垂直,如果一个平面内有一条直线垂直于这两个平面的交线,那么这条直线与另一个平面垂直.用符号语言表示如下:本探究问题的方法包含了两个层次:1.将面面关系转化为线面关系;2.在一个平面内研究线线关系,再从线线关系出发研究线面关系.这样做更加易于学生接受.进一步熟悉平面与平面垂直的概念以及线面垂直的判定定理.实现定理三种语言之间的统一,便于学生直观理解.已知平面,直线.若,且,则有用图形表示如下图:这个定理说明,由平面与平面垂直可以得到直线与平面垂直.这个定理可以用于解决现实生活中的问题.例如,装修房...