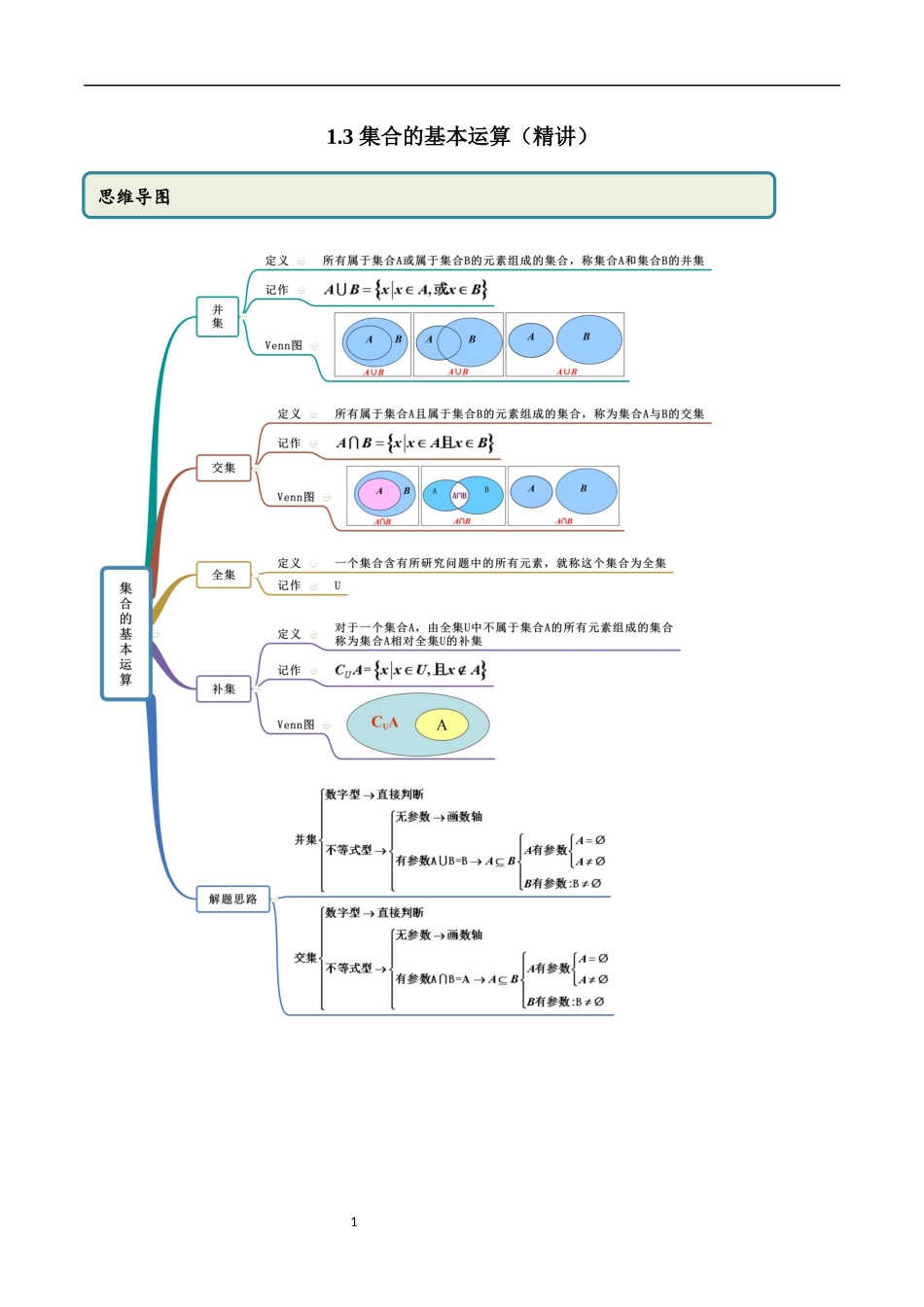
11.3集合的基本运算(精讲)思维导图2考点一交集【例1】(1)(2020·上海高一开学考试)设集合,集合,则等于()A.B.C.D.(2)(2020·安徽省庐江金牛中学)已知集合,,则()A.B.C.D.【答案】(1)A(2)C【解析】(1)集合,集合,又集合与集合中的公共元素为,,故选A.(2)集合,.故选:C.常见考法3【一隅三反】1.(2020·全国高一课时练习)设集合,,则()A.B.C.D.【答案】D【解析】集合,集合,所以,故选D.2(2020·浙江省兰溪市第三中学高三开学考试)已知集合,,则()A.B.C.D.【答案】C【解析】,,又,所以,故本题选C.3.(2020·湖南怀化高二期末)设集合,,则()A.B.C.D.1.交集:两个集合的相同部分的元素所组成的集合2.单个数字交集找相同,不等式的交集画数轴,不同集合高度画不同。4【答案】A【解析】由题意得,,,则,故选:A.考法二并集【例2】(2020·甘肃城关.兰大附中高三月考(理))若集合,,则()A.B.C.D.【答案】D【解析】因为,,所以.故选:D.【一隅三反】1.(2020·贵州南明贵阳一中高三其他(理))已知集合,若,则B可能是()A.B.C.D.【答案】A【解析】因为,所以,四个选项中只有是集合A的子集.故选:A2(2020·上海高一课时练习)满足条件的所有集合A的个数是()A.1B.2C.3D.4【答案】D并集:两个集合所有元素集中在一起的集合,但是重复元素只写一次,要满足集合中的互异性5【解析】因为,所以,集合A可能为,即所有集合A的个数是4,故选D.3.(2019·浙江高一期中)已知集合,,那么=()A.B.C.D.【答案】C【解析】因为,,所以,故选:C考法三补集与全集【例3】(2020·上海高一课时练习)已知全集U={1,3,5,7,9},集合A={1,|a-5|,9},∁UA={5,7},则a的值是()A.2B.8C.-2或8D.2或8【答案】D【解析】由由已知得;故选D【一隅三反】1.(2020·全国高一)设集合,集合,若,则实数_____.【答案】-3【解析】因为集合,,A={0,3},故m=-3.2.(2020·全国高一专题练习)已知全集,则的值为__________【答案】2易错点:并不是所有的全集都是用字母U表示,也不是都是R,要看题目的。6【解析】由补集概念及集合中元素互异性知a应满足分两种情况进行讨论:在A中,由(1)得a=0依次代入(2)、(3)、(4)检验,不合②,故舍去.在B中,由(1)得a=-3,a=2,分别代入(2、(3)、(4)检验,a=-3不合②,故舍去,a=2能满足②③④,故a=2符合题意.答案为:23.(2019·...